题目内容
已知函数![]() 。
。
(1) 若![]() ,求
,求![]()
![]()
![]() +
+![]() 在
在![]() [2,3]上的最小值;
[2,3]上的最小值;
(2) 当![]() 时,求函数
时,求函数![]()
![]() 在
在![]() [1,6]上的最小值。
[1,6]上的最小值。
解⑴对于![]() =2,x∈[2,3],f (x)=e|x–3|+e|x–2|+1=e3–x+ex–1≥2
=2,x∈[2,3],f (x)=e|x–3|+e|x–2|+1=e3–x+ex–1≥2![]() =2e, 当且仅当e3–x=ex–1,即x=2时等号成立,∴f (x)min=2e。
=2e, 当且仅当e3–x=ex–1,即x=2时等号成立,∴f (x)min=2e。
(2)g (x)= ![]() =
=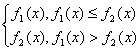 ………9'
………9'
∵![]() 的底数都同为e ,外函数都单调递增
的底数都同为e ,外函数都单调递增
∴比较![]() 的大小关系,只须比较|x–2
的大小关系,只须比较|x–2![]() +1|与|x–
+1|与|x–![]() |+1的大小关系
|+1的大小关系
令![]() |x–2
|x–2![]() +1|,
+1|,![]() |x–
|x–![]() |+1,
|+1,
G (x) =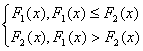 其中
其中![]() ,
,![]() [1,6]
[1,6]
∵![]() ∴2
∴2![]() -1≥
-1≥![]() ≥1
≥1
 令2
令2![]() -1-x=1,得x=2
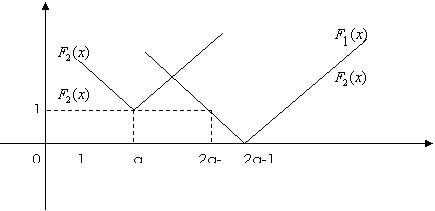
-1-x=1,得x=2![]() -2, 由题意可以如下图象:
-2, 由题意可以如下图象:
当4≤![]() ≤6时,
≤6时,![]() ≤6≤2
≤6≤2![]() –2,G (x)min=F2(
–2,G (x)min=F2(![]() )=1,g (x)min = e 1= e ;
)=1,g (x)min = e 1= e ;

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
已知函数f(x)=
+
的定义域是( )
| 1-x2 |
| x2-1 |
| A、[-1,1] |
| B、{-1,1} |
| C、(-1,1) |
| D、(-∞,-1]∪[1,+∞) |