题目内容
已知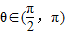 ,
,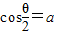 ,则
,则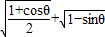 = .
= .
【答案】分析:根据二倍角的三角函数公式,结合“1的代换”化简得原式=|cos |+|
|+|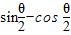 |.由θ的范围化简得原式等于sin
|.由θ的范围化简得原式等于sin ,最后利用同角三角函数的关系,即可算出所求的值.
,最后利用同角三角函数的关系,即可算出所求的值.
解答:解:∵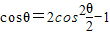
∴1+cosθ=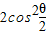 ,可得
,可得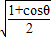 =
=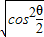 =|cos
=|cos |
|
又∵sinθ=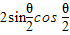 ,1=
,1=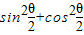
∴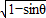 =
=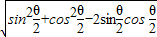 =
=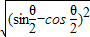 =|
=|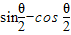 |
|
∵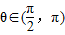 ,可得cos
,可得cos >0且
>0且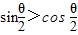
∴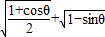 =cos
=cos +(
+(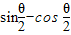 )=sin
)=sin
由同角三角函数的关系,可得sin =
=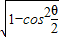 =
=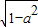
故答案为: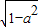
点评:本题给出θ的范围和 的余弦值,求关于θ的三角函数式的值.着重考查了三角函数恒等变换的公式、同角三角函数基本关系等知识,属于中档题.
的余弦值,求关于θ的三角函数式的值.着重考查了三角函数恒等变换的公式、同角三角函数基本关系等知识,属于中档题.
 |+|
|+|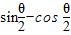 |.由θ的范围化简得原式等于sin
|.由θ的范围化简得原式等于sin ,最后利用同角三角函数的关系,即可算出所求的值.
,最后利用同角三角函数的关系,即可算出所求的值.解答:解:∵
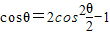
∴1+cosθ=
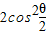 ,可得
,可得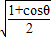 =
=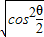 =|cos
=|cos |
|又∵sinθ=
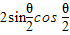 ,1=
,1=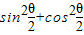
∴
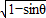 =
=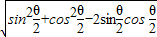 =
=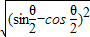 =|
=|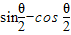 |
|∵
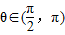 ,可得cos
,可得cos >0且
>0且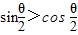
∴
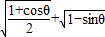 =cos
=cos +(
+(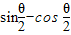 )=sin
)=sin
由同角三角函数的关系,可得sin
 =
=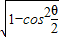 =
=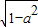
故答案为:
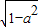
点评:本题给出θ的范围和
 的余弦值,求关于θ的三角函数式的值.着重考查了三角函数恒等变换的公式、同角三角函数基本关系等知识,属于中档题.
的余弦值,求关于θ的三角函数式的值.着重考查了三角函数恒等变换的公式、同角三角函数基本关系等知识,属于中档题. 
练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
已知α∈R,则cos(
+α)=( )
| π |
| 2 |
| A、sinα | B、cosα |
| C、-sinα | D、-cosα |
已知α+β=
,则(1+tanα)(1+tanβ)的值是( )
| π |
| 4 |
| A、-1 | B、1 | C、2 | D、4 |