题目内容
7.已知f(x)=$\left\{\begin{array}{l}{lnx,x>0}\\{-ln(-x),x<0}\end{array}\right.$,若f(a)>f(-a),则实数a的取值范围是(-1,0)∪(1,+∞).分析 由已知中函数的解析式,先分析出函数为奇函数,进而将f(a)>f(-a)转化为f(a)>0,分类讨论可得满足条件的实数a的取值范围.
解答 解:∵f(x)=$\left\{\begin{array}{l}{lnx,x>0}\\{-ln(-x),x<0}\end{array}\right.$,
∴当x>0时,-x<0,
f(-x)=-lnx=-f(x),
当x<0时,-x>0,
f(-x)=ln(-x)=-f(x),
即f(-x)=-f(x)恒成立,
若f(a)>f(-a)时,f(a)>0,
当a>0时,lna>0,a>1,
当a<0时,-ln(-a)>0,即ln(-a)<0,即0<-a<1,即-1<a<0.
综上实数a的取值范围是(-1,0)∪(1,+∞).
故答案为:(-1,0)∪(1,+∞)
点评 本题考查的知识点是分段函数的应用,其中分析出函数为奇函数,进而将f(a)>f(-a)转化为f(a)>0,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.已知圆x2+y2+x+2y=$\frac{61}{16}$和圆(x-sinα)2+(y-1)2=$\frac{1}{16}$,其中0°≤α≤90°,则两圆的位置关系是( )
| A. | 相交 | B. | 外切 | C. | 内切 | D. | 相交或内切 |
19.设全集U={1,2,3,4,5,6,7},P={1,2,3,4},Q={3,4,5,6},则P∩(∁UQ)=( )
| A. | {1,2,3,4,5,6} | B. | {1,2,3,4,5} | C. | {1,2,5} | D. | {1,2} |
17.已知全集U=R,集合A={y|y=2x,x∈R},B={x|x≥2},则下图中阴影部分所表示的集合为( )
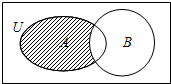

| A. | ∅ | B. | {0,1} | C. | (0,2) | D. | (-∞,2) |
 已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$.
已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的右顶点、上顶点分别为A、B,坐标原点到直线AB的距离为$\frac{{4\sqrt{3}}}{3}$,且$a=\sqrt{2}b$. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为6.