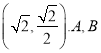题目内容
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() :
:![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 相切,求直线
相切,求直线![]() 的方程;
的方程;
(2)设![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,若存在点
,若存在点![]() ,满足
,满足![]() ,且线段
,且线段![]() 与
与![]() 互相平分(
互相平分(![]() 为原点),求
为原点),求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)联立直线方程与抛物线方程,利用![]() 即可求解。
即可求解。
(2)由直线与抛物线相交可得:![]() ,由(1)可得
,由(1)可得![]()
![]() ,由线段OC与AB互相平分可得四边形OACB为平行四边形,得到C
,由线段OC与AB互相平分可得四边形OACB为平行四边形,得到C![]() ,利用
,利用![]() 得到
得到![]() ,即:
,即:![]()
![]() =-1,再将
=-1,再将![]()
![]() ,
,![]() 代入即可求得
代入即可求得![]() ,对
,对![]() 的范围分类,利用基本不等式即可得解。
的范围分类,利用基本不等式即可得解。
解:(1)法1:由![]() 得
得![]()
![]()
所以,所求的切线方程为![]()
法2:因为直线![]() 恒过(0,-4),所以由
恒过(0,-4),所以由![]() 得
得![]()
设切点为![]() ,由题可得,直线与抛物线在
,由题可得,直线与抛物线在![]() 轴下方的图像相切,
轴下方的图像相切,
则![]()
所以切线方程为![]() ,将坐标(0,-4)代入得
,将坐标(0,-4)代入得![]()
即切点为(8,-8),再将该点代入![]() 得,
得,![]()
所以,所求的切线方程为![]()
(2)由![]() 得
得![]()
![]() 且
且![]() ,
,![]()
![]()
所以![]() ,
,
因为线段OC与AB互相平分,所以四边形OACB为平行四边形
![]()
![]() ,即C
,即C![]()
由![]() 得,
得,![]() ,
,
法1:所以![]()
![]() =-1
=-1
又![]()
 ,又
,又![]()
所以![]()
![]() ,所以
,所以![]()

法2:因为![]()
![]()
又![]()
![]() ,即
,即![]()


【题目】某公司有1000名员工,其中男性员工400名,采用分层抽样的方法随机抽取100名员工进行5G手机购买意向的调查,将计划在今年购买5G手机的员工称为“追光族",计划在明年及明年以后才购买5G手机的员工称为“观望者”,调查结果发现抽取的这100名员工中属于“追光族”的女性员工和男性员工各有20人.
(1)完成下列![]() 列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
列联表,并判断是否有95%的把握认为该公司员工属于“追光族"与“性别"有关;
属于“追光族" | 属于“观望者" | 合计 | |
女性员工 | |||
男性员工 | |||
合计 | 100 |
(2)已知被抽取的这100名员工中有10名是人事部的员工,这10名中有3名属于“追光族”.现从这10名中随机抽取3名,记被抽取的3名中属于“追光族”的人数为随机变量X,求![]() 的分布列及数学期望.
的分布列及数学期望.
附 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |