题目内容
已知函数f(x)=lnx﹣x+1(x∈[1,+∞)),数列{an}满足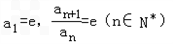 .
.
(1)求数列{an}的通项公式an;
(2)求f(a1)+f(a2)+…+f(an);
(3)求证: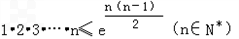 .
.
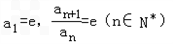 .
.(1)求数列{an}的通项公式an;
(2)求f(a1)+f(a2)+…+f(an);
(3)求证:
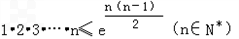 .
.解:(1)∵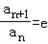 ,
,
∴{an}是等比数列,
又a1=e,∴数列{an}的通项公式为:an=en.
(2)由(1)知,f(an)=lnen﹣en+1=(n+1)﹣en,
∴f(a1)+f(a2)+…+f(an)
=[2+3+…+(n+1)]﹣(e+e2+…+en)
=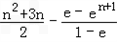 .
.
(3)由函数f(x)=lnx﹣x+1,得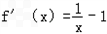 ,
,
又x≥1,∴f'(x)≤0,
∴f(x)递减,∴f(x)≤f(1),
即f(x)≤0,也就是lnx≤x﹣1,
于是:ln1+ln2+…+lnn≤0+1+…+(n﹣1),
即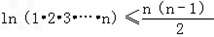 ,
,
故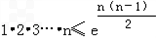 .
.
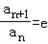 ,
,∴{an}是等比数列,
又a1=e,∴数列{an}的通项公式为:an=en.
(2)由(1)知,f(an)=lnen﹣en+1=(n+1)﹣en,
∴f(a1)+f(a2)+…+f(an)
=[2+3+…+(n+1)]﹣(e+e2+…+en)
=
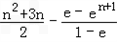 .
.(3)由函数f(x)=lnx﹣x+1,得
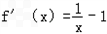 ,
,又x≥1,∴f'(x)≤0,
∴f(x)递减,∴f(x)≤f(1),
即f(x)≤0,也就是lnx≤x﹣1,
于是:ln1+ln2+…+lnn≤0+1+…+(n﹣1),
即
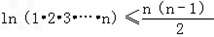 ,
,故
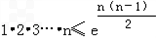 .
.
练习册系列答案
相关题目