题目内容
【题目】已知数列![]() 的各项均为正数,前
的各项均为正数,前![]() 项和
项和![]() 满足
满足![]() ;数列
;数列![]() 是等比数列,前
是等比数列,前![]() 项和为
项和为![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知等比数列![]() 满足
满足![]() ,
,![]() ,
,![]() ,求数列
,求数列![]() 前
前![]() 项和为
项和为![]() ;
;
(3)若![]() ,且等比数列
,且等比数列![]() 的公比
的公比![]() ,若存在
,若存在![]() ,使得
,使得![]() ,试求
,试求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() (2)
(2)![]() (3)2
(3)2
【解析】
(1)![]() 化为
化为![]() ,由
,由![]() 与
与![]() 关系,即可求出通项;
关系,即可求出通项;
(2)由(1)得![]() ,将已知化为
,将已知化为![]() ,即
,即![]() 是关于
是关于![]() 函数,进而转化为求
函数,进而转化为求![]() 的最值,求出
的最值,求出![]() ,即可求解;
,即可求解;
(3)由(1)(2)![]() ,即为
,即为![]() ,求解关于
,求解关于![]() 的不定方程,构造数列
的不定方程,构造数列![]() ,判断单调性,得出
,判断单调性,得出![]() 的可能值,验证,即可求解.
的可能值,验证,即可求解.
(1)数列![]() 前
前![]() 项和
项和![]() 满足
满足![]() ,
,
即![]() ;
;![]() ,
,
![]() ;
;
![]() ,∵数列
,∵数列![]() 的各项均为正数,
的各项均为正数,
∴![]() ,又
,又![]() ,∴
,∴![]() ,
,![]()
(2).∵等比数列![]() 满足
满足![]() ,
,![]() ,
,
∴![]() ,令
,令![]() ,
,
![]() ,当
,当![]() 时,
时,![]() ,
,
![]() 在
在![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减;
单调递减;
∴![]() ,即
,即![]() ,而
,而![]() ,∴
,∴![]() ,
,
∴![]() 且此时
且此时![]() ,设等比数列
,设等比数列![]() 的公比为
的公比为![]() ,
,
![]() ,
,![]() ,所以数列
,所以数列![]() 前
前![]() 项和为
项和为
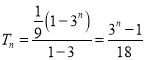 .
.
(3)由![]() ,
,![]() 得:
得:![]() ,
,
正数数列![]() 公比
公比![]() 的等比数列.∵
的等比数列.∵![]() ,
,![]() ,
,
即:![]() ,即:
,即:![]() ,
,
设![]() ,
,![]()
 ,∵
,∵![]() ,
,![]() 时,
时,
上式分子![]() ,
,
数列![]() 单调递增
单调递增
.∴![]() 时,
时,![]() 与
与![]() 矛盾
矛盾
.∴![]() 若
若![]() 时,
时,![]() (∵
(∵![]() )
)
故![]() ,
,![]() 解得
解得![]() 符合条件.
符合条件.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目