题目内容
13.已知定义在R上的奇函数f(x),当x>0时,f(x)=-x2+2x.(1)求函数 f(x)在R上的解析式;
(2)画出函数f(x)的图象,并求出其单调区间.
分析 (1)由函数的奇偶性和已知解析式,把-x整体代入可得解析式;
(2)由(1)画出函数f(x)的图象,数形结合可得单调区间.
解答  解:(1)∵f(x)是定义在R上的奇函数,∴f(0)=0,
解:(1)∵f(x)是定义在R上的奇函数,∴f(0)=0,
当x<0时,-x>0,∴f(x)=-f(-x)=x2+2x,
∴函数 f(x)在R上的解析式为$\left\{\begin{array}{l}{-{x}^{2}+2x,x≥0}\\{{x}^{2}+2x,x<0}\end{array}\right.$;
(2)由(1)画出函数f(x)的图象(如图),
数形结合可得函数f(x)的单调递增区间为(-1,1),
单调递减区间为(-∞,-1)和(1,+∞)
点评 本题考查函数的解析式求解,涉及函数的奇偶性和单调性以及函数的作图,属中档题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
3.若直线(m+3)x+(m2-3)y-2m=0在x轴上的截距是1,则实数m的值等于( )
| A. | -1 | B. | 1 | C. | -3 | D. | 3 |
4.数列{an}中,a1∈Z,an+1=an+log2(1-$\frac{1}{n+1}$),则使{an}为整数的n的取值可能是( )
| A. | 1022 | B. | 1023 | C. | 1024 | D. | 1025 |
8.在区间(-∞,0)上单调递增的函数是( )
| A. | y=2x | B. | y=log2x | C. | y=$\frac{2}{x}$ | D. | y=-2x |

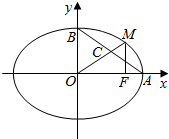 如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.
如图所示,A,B分别是椭圆的右、上顶点,C是AB的三等分点(靠近点B),F为椭圆的右焦点,OC的延长线交椭圆于点M,且MF⊥OA,则椭圆的离心率为$\frac{\sqrt{5}}{5}$.