题目内容
【题目】已知直线系方程![]() (其中
(其中![]() 为参数).当
为参数).当![]() 时,直线
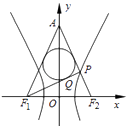
时,直线![]() 与两坐标轴所围成的三角形的面积为__________,若该直线系中的三条直线围成正三角形区域
与两坐标轴所围成的三角形的面积为__________,若该直线系中的三条直线围成正三角形区域![]() ,则区域
,则区域![]() 的面积为__________.
的面积为__________.
【答案】 ![]()
![]() 或
或![]()
【解析】当![]() 时,直线为
时,直线为![]() ,即
,即![]() ,当
,当![]() 时,
时, ![]() ,与
,与![]() 轴交于
轴交于![]() 点,当
点,当![]() 时,
时, ![]() ,与
,与![]() 轴交于
轴交于![]() 点,∴直线
点,∴直线![]() 与两坐标轴围成的三角形面积
与两坐标轴围成的三角形面积![]() ,设直线系中三条直线围成的是正三角形区域
,设直线系中三条直线围成的是正三角形区域![]() ,先把整个直线系向下平移一个单位,这个区域
,先把整个直线系向下平移一个单位,这个区域![]() 不会变,直线系方程变为
不会变,直线系方程变为![]() ,如果令
,如果令![]() ,
, ![]() ,带入上面方程,等式成立,因此
,带入上面方程,等式成立,因此![]() 是直线上的点对于某个固定的
是直线上的点对于某个固定的![]() ,注意到
,注意到![]() ,
, ![]() 是以原点为圆心,半径为
是以原点为圆心,半径为![]() 的圆的参数方程,而
的圆的参数方程,而![]() 恰好是此圆的切线,因此直线方程
恰好是此圆的切线,因此直线方程![]() 都是这个圆的切线的集合,那么这些切线组成的正三角形有两种情况,如果圆是这个正三角形的内切圆,面积是
都是这个圆的切线的集合,那么这些切线组成的正三角形有两种情况,如果圆是这个正三角形的内切圆,面积是![]() ,如果圆是正三角形的旁切元,面积是
,如果圆是正三角形的旁切元,面积是![]() ,故答案为(1)
,故答案为(1) ![]() (2)
(2) ![]() 或
或![]() .
.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目