题目内容
已知抛物线y2=2px（p＞0）的焦点为F，过点F且斜率为k的直线l与该抛物线分别交于A、B两点（点A在第一象限），若
=3
，则k=（ ）
| AF |
| FB |
分析：根据题意，作出抛物线与直线AB的图象，利用抛物线的定义将曲线上的点到焦点的距离转化为曲线上的点到准线的距离，借助几何图形可判断直线AB的倾斜角，从而可得答案．
解答：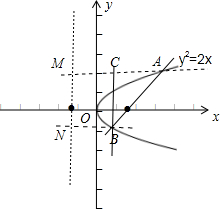
解：过A、B分别作准线的垂线，垂足分别为M，N，作BC⊥AM，垂足为C，
设|
|=m，|
|=3m，则
由抛物线的定义得|AM|=3m，|BN|=m，
∴|
|=4m，|
|=2m，
∴∠BAC=60°，于是直线l的倾斜角为60°，斜率k=
故选A．
解：过A、B分别作准线的垂线，垂足分别为M，N，作BC⊥AM，垂足为C，设|
| FB |
| AF |
由抛物线的定义得|AM|=3m，|BN|=m，
∴|
| AB |
| AC |
∴∠BAC=60°，于是直线l的倾斜角为60°，斜率k=
| 3 |
故选A．
点评：本题考查抛物线的概念，突出考查抛物线定义的灵活运用，体现转化思想的妙用，属于中档题．
练习册系列答案
相关题目