题目内容
从原点O引直线交直线2x+4y-1=0于点M，P为OM上一点，已知|OP|·|OM|=1，求P点的极坐标方程.
思路分析:先把直线化为极坐标方程,由于P点的运动与M点有关,可以利用转移法来解决问题.我们可以根据长度之间的关系式找到点P与点M坐标之间的关系.
解:如图,以O为极点,x轴正方向为极轴建立坐标系后,直线的方程化为2ρcosθ+4ρsinθ-1=0.
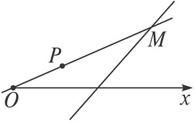
设M(ρ0,θ0),P(ρ,θ),
则2ρ0cosθ0+4ρ0sinθ0-1=0.
又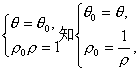
∴2
cosθ+4
sinθ-1=0.
∴ρ=2cosθ+4sinθ,这是一个圆(ρ≠0).
练习册系列答案
阅读快车系列答案
相关题目
设双曲线
-
=1（a＞0，b＞0）的右顶点为A，P为双曲线上的一个动点（不是顶点），从点A引双曲线的两条渐近线的平行线，与直线OP分别交于Q，R两点，其中O为坐标原点，则|OP|2与|OQ|•|OR|的大小关系为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| A、|OP|2＜|OQ|•|OR| |
| B、|OP|2＞|OQ|•|OR| |
| C、|OP|2=|OQ|•|OR| |
| D、不确定 |