题目内容
已知函数f(x)的图象与函数h(x)= 的图象关于点A(1,0)对称.
的图象关于点A(1,0)对称.
(1)求函数f(x)的解析式;
(2)若g(x)=f(x)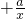 ,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
,g(x)在区间(0,2]上的值不小于6,求实数a的取值范围.
解:(1)设函数f(x)的图象上的任意一点C(x,y),
点C(x,y)关于点A(1,0)对称的点为B(x1,y1),
∴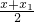 =1,
=1,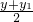 =0,解得x1=2-x,y1=-y,
=0,解得x1=2-x,y1=-y,
∵函数f(x)的图象与函数h(x)= 的图象关于点A(1,0)对称,
的图象关于点A(1,0)对称,
∴点B(2-x,-y),在数h(x)= 的图象上,代入得f(x)的解析式:
的图象上,代入得f(x)的解析式:
∴-y=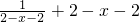 =-
=- -2,
-2,
∴y= +x,∴函数f(x)的解析式f(x)=y=
+x,∴函数f(x)的解析式f(x)=y= +x
+x
∴f(x)=x+
(2)由g(x)=f(x)+ =x+
=x+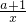 ≥6,
≥6,
得a≥-x2+6x-1在(0,2]上恒成立,所以
a≥(-x2+6x-1)max,
∵-x2+6x-1=-(x-3)2+8在(0,2]上的最大值为x=2时取得,
∴(-x2+6x-1)max=7,
∴实数a的取值范围a≥7;
分析:(1)设任一点C在f(x)上,求出点C关于点A(1,0)对称点B,根据题意点B在函数h(x)= 的图象上,代入即可求出函数f(x)的解析式;
的图象上,代入即可求出函数f(x)的解析式;
(2)把f(x)代入g(x),要求g(x)在区间(0,2]上的值不小于6,等价转化为a≥-x2+6x-1在(0,2]上恒成立,从而求出a的范围;
点评:此题考查了图形的中心对称以及函数的恒成立问题,体现一种转化的思想,我要认真体会,此题是一道中档题;
点C(x,y)关于点A(1,0)对称的点为B(x1,y1),
∴
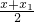 =1,
=1,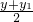 =0,解得x1=2-x,y1=-y,
=0,解得x1=2-x,y1=-y,∵函数f(x)的图象与函数h(x)=
 的图象关于点A(1,0)对称,
的图象关于点A(1,0)对称,∴点B(2-x,-y),在数h(x)=
 的图象上,代入得f(x)的解析式:
的图象上,代入得f(x)的解析式:∴-y=
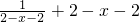 =-
=- -2,
-2,∴y=
 +x,∴函数f(x)的解析式f(x)=y=
+x,∴函数f(x)的解析式f(x)=y= +x
+x∴f(x)=x+

(2)由g(x)=f(x)+
 =x+
=x+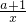 ≥6,
≥6,得a≥-x2+6x-1在(0,2]上恒成立,所以
a≥(-x2+6x-1)max,
∵-x2+6x-1=-(x-3)2+8在(0,2]上的最大值为x=2时取得,
∴(-x2+6x-1)max=7,
∴实数a的取值范围a≥7;
分析:(1)设任一点C在f(x)上,求出点C关于点A(1,0)对称点B,根据题意点B在函数h(x)=
 的图象上,代入即可求出函数f(x)的解析式;
的图象上,代入即可求出函数f(x)的解析式;(2)把f(x)代入g(x),要求g(x)在区间(0,2]上的值不小于6,等价转化为a≥-x2+6x-1在(0,2]上恒成立,从而求出a的范围;
点评:此题考查了图形的中心对称以及函数的恒成立问题,体现一种转化的思想,我要认真体会,此题是一道中档题;

练习册系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(