题目内容
已知函数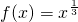 ,函数g(x)=-x2+3x,则方程f(x)=g(x)在实数范围内解的个数为________个.
,函数g(x)=-x2+3x,则方程f(x)=g(x)在实数范围内解的个数为________个.
4
分析:函数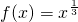 是奇函数且是单调增函数,函数g(x)=-x2+3x的图象是开口向下的抛物线,由此只要在同一坐标系中作出两个函数的图象,观察它们的交点的个数,就可得出方程f(x)=g(x)在实数范围内解的个数.
是奇函数且是单调增函数,函数g(x)=-x2+3x的图象是开口向下的抛物线,由此只要在同一坐标系中作出两个函数的图象,观察它们的交点的个数,就可得出方程f(x)=g(x)在实数范围内解的个数.
解答:在同一坐标系中作出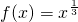

和g(x)=-x2+3x的图象,
发现x=0是它们的一个公共点.
再看两个函数的图象
在x<0的情况下有一个公共点;在在x>0的情况下有两个个公共点
可得两个函数图象的公共点的个数为4个
故答案为4
点评:本题考查了方程的根的个数的问题,属于中档题.采用数形结合的方法,观察两函数图象的公共点的个数,找到方程个数,是这类问题常用的方法.
分析:函数
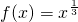 是奇函数且是单调增函数,函数g(x)=-x2+3x的图象是开口向下的抛物线,由此只要在同一坐标系中作出两个函数的图象,观察它们的交点的个数,就可得出方程f(x)=g(x)在实数范围内解的个数.
是奇函数且是单调增函数,函数g(x)=-x2+3x的图象是开口向下的抛物线,由此只要在同一坐标系中作出两个函数的图象,观察它们的交点的个数,就可得出方程f(x)=g(x)在实数范围内解的个数.解答:在同一坐标系中作出
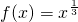

和g(x)=-x2+3x的图象,
发现x=0是它们的一个公共点.
再看两个函数的图象
在x<0的情况下有一个公共点;在在x>0的情况下有两个个公共点
可得两个函数图象的公共点的个数为4个
故答案为4
点评:本题考查了方程的根的个数的问题,属于中档题.采用数形结合的方法,观察两函数图象的公共点的个数,找到方程个数,是这类问题常用的方法.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
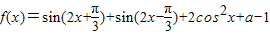 (a为常数),若函数f(x)的最大值为
(a为常数),若函数f(x)的最大值为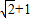 .
.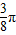 个单位,再向下平移2个单位得到函数y=g(x)的图象,求函数g(x)的单调递减区间.
个单位,再向下平移2个单位得到函数y=g(x)的图象,求函数g(x)的单调递减区间.