题目内容
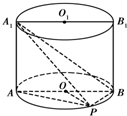 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.(Ⅰ)求证:平面A1PB⊥平面A1AP;
(Ⅱ)在三棱锥A1-APB的6条棱中,任取2条棱,求恰好能互相垂直的概率.
分析:(I)利用直径所对的圆周角等于90°,可证AP⊥BP,再证线面垂直,然后由线面垂直证明面面垂直;
(II)由(I)的线面垂直,可得三棱锥的六条棱中,线线垂直的情况,利用古典概型概率公式计算.
(II)由(I)的线面垂直,可得三棱锥的六条棱中,线线垂直的情况,利用古典概型概率公式计算.
解答:解:(I)∵A1A⊥平面PAB.PB?平面PAB,∴AA1⊥PB;
又∵点P在圆柱OO1的底面圆O上,AB是直径,∴AP⊥PB;
AA1∩AP=A,∴PB⊥平面A1AP,PB?平面A1PB,
∴平面AA1P⊥平面A1PB;
(II)在三棱锥A1-APB的6条棱中,AA1⊥AB;AA1⊥AP;AA1⊥BP;
由(I)知:BP⊥A1P;BP⊥AP.共5组棱互相垂直的情况,
∴任取2条棱,求恰好能互相垂直的概率为
=
=
.
又∵点P在圆柱OO1的底面圆O上,AB是直径,∴AP⊥PB;
AA1∩AP=A,∴PB⊥平面A1AP,PB?平面A1PB,
∴平面AA1P⊥平面A1PB;
(II)在三棱锥A1-APB的6条棱中,AA1⊥AB;AA1⊥AP;AA1⊥BP;
由(I)知:BP⊥A1P;BP⊥AP.共5组棱互相垂直的情况,
∴任取2条棱,求恰好能互相垂直的概率为
| 5 | ||
|
| 5 |
| 15 |
| 1 |
| 3 |
点评:本题考查了面面垂直的判定,线面垂直的性质,考查了古典概型的概率计算,解题的关键是由线面垂直判定线线垂直的情况数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
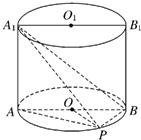 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.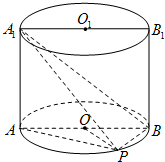 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为20π,OA=2,∠AOP=120°.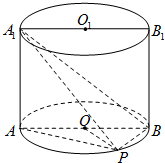 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,圆柱OO1的表面积为24π,OA=2,∠AOP=120°.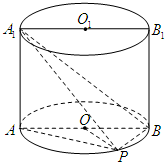 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为