题目内容
已知焦点在x轴上的抛物线C经过点(3,6).
(1)求抛物线C的标准方程;
(2)直线l:y=kx-3过抛物线C的焦点且与抛物线C交于A、B两点,求A、B两点距离.
(1)求抛物线C的标准方程;
(2)直线l:y=kx-3过抛物线C的焦点且与抛物线C交于A、B两点,求A、B两点距离.
分析:(1)设抛物线方程为y2=ax,利用抛物线C经过点(3,6),求出a的值,即可求抛物线C的标准方程;
(2)求得直线l方程,与抛物线方程联立,求出A,B的坐标,即可求得A、B两点距离.
(2)求得直线l方程,与抛物线方程联立,求出A,B的坐标,即可求得A、B两点距离.
解答:解:(1)设抛物线方程为y2=ax
∵抛物线C经过点(3,6),
∴36=3a,∴a=12
∴抛物线C的标准方程为y2=12x;
(2)将焦点(3,0)代入y=kx-3得直线l方程为y=x-3,
由
消去x可得y2-12y+36=0,∴y=6±6
∴x=9±6
∴|AB|=
=24.
∵抛物线C经过点(3,6),
∴36=3a,∴a=12
∴抛物线C的标准方程为y2=12x;
(2)将焦点(3,0)代入y=kx-3得直线l方程为y=x-3,
由
|
| 2 |
∴x=9±6
| 2 |
∴|AB|=
| 288+288 |
点评:本题考查抛物线的标准方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
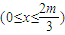 和椭圆弧
和椭圆弧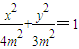

 和椭圆弧
和椭圆弧
