题目内容
16.过两条直线x-2y+3=0和x+2y-9=0的交点和原点的直线的方程是x-y=0.分析 先求出两直线的交点坐标,再利用两点式方程能求出所求的直线方程.
解答 解:解方程组$\left\{\begin{array}{l}{x-2y+3=0}\\{x+2y-9=0}\end{array}\right.$,得x=3,y=3,
∴两条直线x-2y+3=0和x+2y-9=0的交点为(3,3),
原点坐标为(0,0),
∴过两条直线x-2y+3=0和x+2y-9=0的交点和原点的直线的方程是:
$\frac{y}{x}=\frac{3}{3}$,即x-y=0.
故答案为:x-y=0.
点评 本题考查直线方程的求法,是基础题,解题时要认真审题,注意两点式子直线方程的合理运用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
7.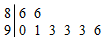 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
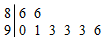 如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )
如图是某班8为学生诗词比赛得分的茎叶图,那么这8为学生得分的众数和中位数分别为( )| A. | 93,91 | B. | 86,93 | C. | 93,92 | D. | 86,91 |
1.(5)若xy满足约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{y+2≥0}\\{x+y+2≤0}\end{array}\right.$,则$\frac{y+1}{x-1}$的取值范围为( )
| A. | [-$\frac{1}{3}$,$\frac{1}{5}$] | B. | [-$\frac{1}{3}$,1] | C. | (-∞,-$\frac{1}{3}$]∪[$\frac{1}{5}$,+∞) | D. | (-∞,-$\frac{1}{3}$]∪[1,+∞) |