题目内容
已知M是以F1,F2为焦点的椭圆 上的一点,O是坐标原点,若2MO=F1F2,则△F1MF2的面积是 .
上的一点,O是坐标原点,若2MO=F1F2,则△F1MF2的面积是 .
【答案】分析:根据2MO=F1F2,可推断△F1MF2为直角三角形,设F1M=m,MF2=n,根据勾股定理可知m2+n2=4c2,根据椭圆定义可知m+n=2a,进而根据mn=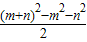 求得nm的值,最后根据直角三角形面积公式求得答案.
求得nm的值,最后根据直角三角形面积公式求得答案.
解答:解:∵2MO=F1F2,
∴∠F1MF2=90°
设F1M=m,MF2=n
∴m2+n2=16
根据椭圆定义可知m+n=2a=2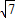
∴mn=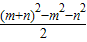 =6
=6
∴△F1MF2的面积是 ab=3
ab=3
故答案为3
点评:本题主要考查了椭圆的应用.解题的关键是根据2MO=F1F2判断△F1MF2为直角三角形.
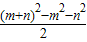 求得nm的值,最后根据直角三角形面积公式求得答案.
求得nm的值,最后根据直角三角形面积公式求得答案.解答:解:∵2MO=F1F2,
∴∠F1MF2=90°
设F1M=m,MF2=n
∴m2+n2=16
根据椭圆定义可知m+n=2a=2
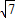
∴mn=
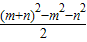 =6
=6∴△F1MF2的面积是
 ab=3
ab=3故答案为3
点评:本题主要考查了椭圆的应用.解题的关键是根据2MO=F1F2判断△F1MF2为直角三角形.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 上的一点,O是坐标原点,若2MO=F1F2,则△F1MF2的面积是 .
上的一点,O是坐标原点,若2MO=F1F2,则△F1MF2的面积是 .