题目内容
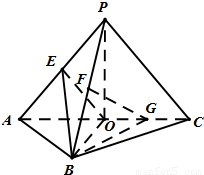
如图,△PAC与△ABC是均以AC为斜边的等腰直角三角形,AC=4,E,F,O分别为PA,PB,AC的中点,G为OC的中点,且PO⊥平面ABC.(1)证明:FE∥平面BOG;
(2)求二面角EO-B-FG的余弦值.
【答案】分析:(1)通过建立空间直角坐标系,利用平面BOE的法向量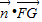 =0即可证明;
=0即可证明;
(2)利用两个平面的法向量的夹角公式即可得出.
解答:(1)证明:以O点为坐标原点,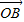 ,
,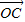 ,
, 的方向为x轴,y轴,z轴的正方向建立空间直角坐标系数,
的方向为x轴,y轴,z轴的正方向建立空间直角坐标系数,
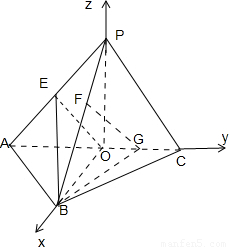 则O(0,0,0),B(2,0,0),C(0,2,0),A(0,-2,0),P(0,0,2),G(0,1,0),E(0,-1,1),F(1,0,1).
则O(0,0,0),B(2,0,0),C(0,2,0),A(0,-2,0),P(0,0,2),G(0,1,0),E(0,-1,1),F(1,0,1).
∴ ,
, ,
,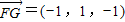 .
.
设平面OBE的法向量为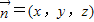 ,
,
则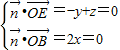 ,令y=1,解得
,令y=1,解得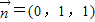 ,
,
∴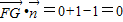 ,∴
,∴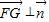 ,
,
∵G∉平面BOE,∴FG∥平面BOE;
(2)由 (1)的证法二可知.平面OBE的法向量为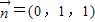 .
.
设平面BGF的法向量为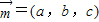 ,又
,又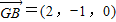 ,
,
则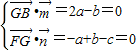 ,令c=1,则
,令c=1,则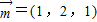 ,
,
设二面角EO-B-FG的平面角为θ,则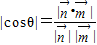 =
=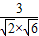 =
=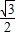
由由图易知二面角EO-B-FG的平面角为锐角,
∴二面角EO-B-FG的余弦值为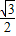 .
.
点评:熟练掌握通过建立空间直角坐标系,利用平面BOE的法向量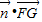 =0、两个平面的法向量的夹角公式求二面角的平面角等是解题的关键.
=0、两个平面的法向量的夹角公式求二面角的平面角等是解题的关键.
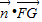 =0即可证明;
=0即可证明;(2)利用两个平面的法向量的夹角公式即可得出.
解答:(1)证明:以O点为坐标原点,
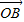 ,
,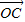 ,
,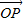 的方向为x轴,y轴,z轴的正方向建立空间直角坐标系数,
的方向为x轴,y轴,z轴的正方向建立空间直角坐标系数, 则O(0,0,0),B(2,0,0),C(0,2,0),A(0,-2,0),P(0,0,2),G(0,1,0),E(0,-1,1),F(1,0,1).
则O(0,0,0),B(2,0,0),C(0,2,0),A(0,-2,0),P(0,0,2),G(0,1,0),E(0,-1,1),F(1,0,1).∴
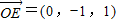 ,
,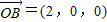 ,
,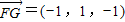 .
.设平面OBE的法向量为
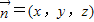 ,
,则
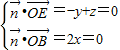 ,令y=1,解得
,令y=1,解得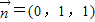 ,
,∴
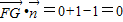 ,∴
,∴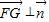 ,
,∵G∉平面BOE,∴FG∥平面BOE;
(2)由 (1)的证法二可知.平面OBE的法向量为
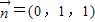 .
.设平面BGF的法向量为
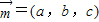 ,又
,又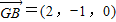 ,
,则
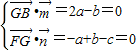 ,令c=1,则
,令c=1,则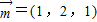 ,
,设二面角EO-B-FG的平面角为θ,则
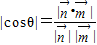 =
=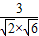 =
=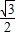
由由图易知二面角EO-B-FG的平面角为锐角,
∴二面角EO-B-FG的余弦值为
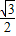 .
.点评:熟练掌握通过建立空间直角坐标系,利用平面BOE的法向量
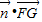 =0、两个平面的法向量的夹角公式求二面角的平面角等是解题的关键.
=0、两个平面的法向量的夹角公式求二面角的平面角等是解题的关键. 
练习册系列答案
相关题目
 22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.
22、如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B,C两点,圆心O在∠PAC的内部,点M是BC的中点.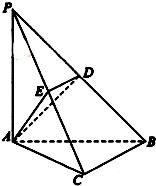 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱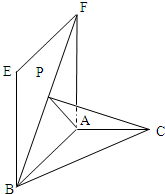 (2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=
(2008•湖北模拟)如图,直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=

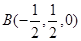 ,P(0,0,2).
,P(0,0,2).
 ,
, 于是
于是 ,所以
,所以
 设平面PCD的法向量
设平面PCD的法向量 ,
, ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
. .
. ,由此得
,由此得 .
.
 ,解得
,解得 ,即
,即 .
. ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以
 于点H,连接DH.由
于点H,连接DH.由 ,可得
,可得 .
. ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
 所以二面角
所以二面角 的正弦值为
的正弦值为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

 中,由
中,由 ,
, ,
,
 .由余弦定理,
.由余弦定理, ,
,