Question

已知函数f(x)＝log₄(4^x＋1)＋kx(k∈R)为偶函数.

(1)求k的值；

(2)若方程f(x)＝log₄(a·2^x－a)有且只有一个根，求实数a的取值范围.

Answer 1

(1)因为f(x)为偶函数，所以f(－x)＝f(x)，

log₄(4^－x＋1)－kx＝log₄(4^x＋1)＋kx，

log₄－log₄(4^x＋1)＝2kx⇒(2k＋1)x＝0

⇒k＝－.

(2)依题意知：log₄(4^x＋1)－x＝log₄(a·2^x－a)

⇒，

令t＝2^x，则(*)变为(1－a)t²＋at＋1＝0只需其有一正根.

①若a＝1，则t＝－1不合题意.

②若(*)式有一正一负根，则，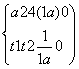

∴a＞1，

经验证知a＞1时满足a·2^x－a＞0，∴a＞1.

③两实根相等，Δ＝0⇒a＝±2－2.

当a＝－2－2时，方程(1－a)t²＋at＋1＝0的根为t＝2^x＝

＝＝，

此时满足2^x·a－a＞0.

当a＝2－2时，方程(1－a)t²＋at＋1＝0的根为t＝2^x＝＝

＝，不满足a·2^x－a＞0，

∴a＝－2－2，

综上所述，a＞1或a＝－2－2.