题目内容
4.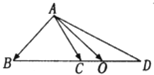 在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )
在△ABC中,点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),若$\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则x的取值范围是( )| A. | (-1,0) | B. | (0,$\frac{1}{3}$) | C. | (0,1) | D. | (-$\frac{1}{3}$,0) |
分析 由已知O,B,C三点共线,所以得到x+y=1,又由$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),利用共面向量基本定理即可得出
解答 解:由已知O,B,C三点共线,所以得到x+y=1,所以 $\overrightarrow{AO}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$=x$\overrightarrow{AB}$+(1-x)$\overrightarrow{AC}$=x($\overrightarrow{AB}-\overrightarrow{AC}$)+$\overrightarrow{AC}$=x$\overrightarrow{CB}$+$\overrightarrow{AC}$,
点D在线段BC的延长线上,且$\overrightarrow{BC}$=$\overrightarrow{CD}$,点O在线段CD上(点O与点C,D不重合),所以x的取值范围为-1<x<0;
故选:A.
点评 本题考查了向量的三角形法则、共线向量定理、共面向量基本定理,考查了推理能力,属于基础题.

练习册系列答案
相关题目
15.已知a>0且a≠1,命题“?x>1,logax>0”的否定是( )
| A. | ?x≤1,logax>0 | B. | ?x>1,loga≤0 | C. | ?x≤1,logax>0 | D. | ?x>1,logax≤0 |
16.设集合A={x||x|≤2},B={y|y=2x,x∈R},则A∩B=( )
| A. | (0,2] | B. | [-2,2) | C. | [0,2) | D. | [2,+∞) |
13.直角三角形ABC中,A为直角,AB=1,BC=2,若点AM是BC边上的高线,点P在△ABC 内部或边界上运动,则$\overrightarrow{AM}$•$\overrightarrow{BP}$的范围是( )
| A. | [-$\frac{\sqrt{3}}{2}$,0] | B. | [-$\frac{3}{4}$,0] | C. | [-$\frac{\sqrt{3}}{4}$,0] | D. | [-3,0] |