题目内容
已知f(x)=ax,(a>1)的导函数是f'(x),记A=f'(a),B=f(a+1)-f(a),C=f'(a+1)则
- A.A>B>C
- B.A>C>B
- C.B>A>C
- D.C>B>A
D
分析:注意到A,B,C具有几何意义,设M坐标为(a,f(a)),N坐标为(a+1,f(a+1)),利用导数及直线斜率的求法得到A、B、C分别为指数函数在M处的斜率,直线MN的斜率及指数函数在N处的斜率,根据指数函数的图象可知大小,得到正确答案.
解答:记M(a,f(a)),N(a+1,f(a+1)),
则由于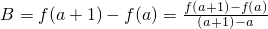 ,表示直线MN的斜率;
,表示直线MN的斜率;
A=f′(a)表示函数f(x)=ax(a>1)在 点M处的切线斜率;
C=f′(a+1)表示函数f(x)=ax(a>1)在点N处的切线斜率.
结合f(x)=ax(a>1)的图象,可得C>B>A.
故选D
点评:此题是代数式大小比较,考查学生能利用导数求过曲线上某点切线的斜率,掌握直线斜率的求法,是一道好题.
分析:注意到A,B,C具有几何意义,设M坐标为(a,f(a)),N坐标为(a+1,f(a+1)),利用导数及直线斜率的求法得到A、B、C分别为指数函数在M处的斜率,直线MN的斜率及指数函数在N处的斜率,根据指数函数的图象可知大小,得到正确答案.
解答:记M(a,f(a)),N(a+1,f(a+1)),
则由于
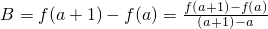 ,表示直线MN的斜率;
,表示直线MN的斜率;A=f′(a)表示函数f(x)=ax(a>1)在 点M处的切线斜率;
C=f′(a+1)表示函数f(x)=ax(a>1)在点N处的切线斜率.
结合f(x)=ax(a>1)的图象,可得C>B>A.
故选D
点评:此题是代数式大小比较,考查学生能利用导数求过曲线上某点切线的斜率,掌握直线斜率的求法,是一道好题.

练习册系列答案
相关题目