题目内容
已知A，B，C是抛物线y2=4x上任意三点，F是抛物线的焦点且| FA |
| FB |
| FC |
| FA |
| FB |
| FC |
分析：由题意可得F（1，0），是三角形ABC的重心，故
=1，再由抛物线的定义可得 |
|+|
|+|
|=xA+1+xB+1+xC+1=3．
| xA+xB+xC |
| 3 |
| FA |
| FB |
| FC |
解答：解：由题意可得F（1，0），是抛物线的焦点，也是三角形ABC的重心，故
=1，
∴xA+xB+xC=3． 再由抛物线的定义可得 |
|+|
|+|
|=xA+1+xB+1+xC+1
=3+3=6，
故答案为6．
| xA+xB+xC |
| 3 |
∴xA+xB+xC=3． 再由抛物线的定义可得 |
| FA |
| FB |
| FC |
=3+3=6，
故答案为6．
点评：本题考查三角形的重心坐标公式，抛物线的定义、标准方程，以及简单性质的应用，求得 xA+xB+xC=3，是
解题的关键．
解题的关键．
练习册系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
已知抛物线型拱桥的顶点距离水面2米时，测量水面宽为8米，当水面上升1米后，水面的宽度是（ ）
| A、1米 | ||
| B、2米 | ||
C、2
| ||
D、4
|
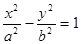
的离心率为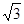
，且它的一条准线与抛物
的准线重合，则此双曲线的方程是( )
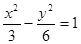B．
D．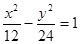
)为方向向量的直线l过点(0, 
(p>0)的顶点关于直线l的对称点在该抛物的准线上．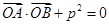
(O为原点，A、B异于原点)，试求点N的轨迹方程．
是抛物
的一条切线.
的动直线L交椭圆C于A、B两点，试问：在坐标平面上是否存在一个定点T，使得以AB为直径的圆恒过点T？若存在，求出点T的坐标；若不存在，请说明理由.
