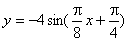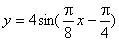题目内容
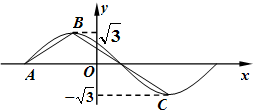 函数
函数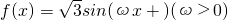 的部分图象,如图所示,若
的部分图象,如图所示,若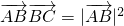 ,则ω等于
,则ω等于
- A.

- B.

- C.

- D.

B
分析:由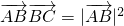 ,可求得∠ABC=120°,再由函数最大值为
,可求得∠ABC=120°,再由函数最大值为 ,通过解三角形可求得周期,由此即可求得ω值.
,通过解三角形可求得周期,由此即可求得ω值.
解答:由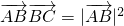 ,得|
,得| |•|
|•| |•cos(π-∠ABC)=
|•cos(π-∠ABC)=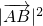 ,即|
,即| |•(-cos∠ABC)=
|•(-cos∠ABC)= ,
,
由图知| |=2|
|=2| |,所以cos∠ABC=-
|,所以cos∠ABC=- ,即得∠ABC=120°,
,即得∠ABC=120°,
过B作BD⊥x轴于点D,则BD= ,在△ABD中∠ABD=60°,BD=
,在△ABD中∠ABD=60°,BD= ,易求得AD=3,
,易求得AD=3,
所以周期T=3×4=12,所以ω= =
= .
.
故选B.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式及平面向量数量积的运算,解决本题的关键是由所给数量积求出∠ABC=120°.
分析:由
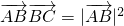 ,可求得∠ABC=120°,再由函数最大值为
,可求得∠ABC=120°,再由函数最大值为 ,通过解三角形可求得周期,由此即可求得ω值.
,通过解三角形可求得周期,由此即可求得ω值.解答:由
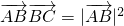 ,得|
,得| |•|
|•| |•cos(π-∠ABC)=
|•cos(π-∠ABC)=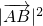 ,即|
,即| |•(-cos∠ABC)=
|•(-cos∠ABC)= ,
,由图知|
 |=2|
|=2| |,所以cos∠ABC=-
|,所以cos∠ABC=- ,即得∠ABC=120°,
,即得∠ABC=120°,过B作BD⊥x轴于点D,则BD=
 ,在△ABD中∠ABD=60°,BD=
,在△ABD中∠ABD=60°,BD= ,易求得AD=3,
,易求得AD=3,所以周期T=3×4=12,所以ω=
 =
= .
.故选B.
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式及平面向量数量积的运算,解决本题的关键是由所给数量积求出∠ABC=120°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
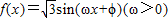 的部分图象,如图所示,若
的部分图象,如图所示,若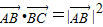 ,则ω等于( )
,则ω等于( )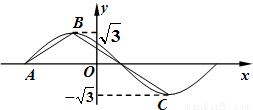
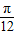
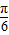
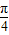
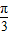
 的部分图象,如图所示,若
的部分图象,如图所示,若 ,则ω等于( )
,则ω等于( )




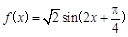 ,
,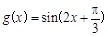 ,
,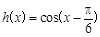 的部分图象(如图),则( )
的部分图象(如图),则( )
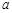 为
为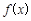 ,
,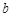 为
为 ,
,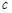 为
为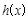
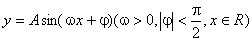 的部分图象,
的部分图象,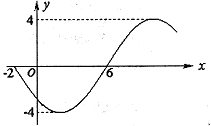 如图所示,则函数表达式为
( )
如图所示,则函数表达式为
( )