题目内容
球面上三点A，B，C组成这个球的一个截面的内接三角形，AB=18，BC=24，AC=30，且球心到该截面的距离为球的半径的一半．
（1）求球的体积；
（2）求A，C两点的球面距离．
解：（1）球面上三点A、B、C，平面ABC与球面交于一个圆，三点A、B、C在这个圆上
∵AB=18，BC=24，AC=30，AC2=AB2+BC2，
∴AC为这个圆的直径，AC中点M圆心球心O到平面ABC的距离，即OM=球半径的一半=
R，
在△OMA中，∠OMA=90°OM=R，AM=AC=15，OA=R
由勾股定理（R）2+152=R2，
R2=225 R2=300，R=10
球的体积S=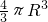
=4000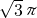
（体积单位）．
（2）由（1）可知∠AOC=120°
所以A，C两点的球面距离：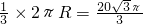
分析：（1）通过题意，确定△ABC的形状，先求球的半径，然后求球的体积．
（2）求出∠AOC，再求A，C两点的球面距离．
点评：本题考查球的体积及其他计算，考查学生空间想象能力，是中档题．
∵AB=18，BC=24，AC=30，AC2=AB2+BC2，
∴AC为这个圆的直径，AC中点M圆心球心O到平面ABC的距离，即OM=球半径的一半=
R，在△OMA中，∠OMA=90°OM=
R，AM=AC=15，OA=R由勾股定理（
R）2+152=R2，R2=225 R2=300，R=10球的体积S=
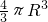=4000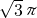（体积单位）．（2）由（1）可知∠AOC=120°
所以A，C两点的球面距离：
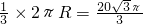
分析：（1）通过题意，确定△ABC的形状，先求球的半径，然后求球的体积．
（2）求出∠AOC，再求A，C两点的球面距离．
点评：本题考查球的体积及其他计算，考查学生空间想象能力，是中档题．
练习册系列答案
相关题目
过球面上三点A、B、C的截面和球心的距离是球半径的一半，且AB=6，BC=8，AC=10，则球的表面积是（ ）
| A、100π | ||
| B、300π | ||
C、
| ||
D、
|