题目内容
附加题:定义在R上的函数f(x)满足f(x+1)=2f(x),若当0≤x≤1时,f(x)=x(1-x),则当-1≤x≤0时,f(x)=
-
x(x+1)
| 1 |
| 2 |
-
x(x+1)
.| 1 |
| 2 |
分析:由-1≤x≤0,得0≤x+1≤1,再由题中表达式求得f(x+1),根据f(x+1)=2f(x)从而求得f(x).
解答:解:当-1≤x≤0时,有0≤x+1≤1,
∴f(x+1)=(x+1)[1-(x+1)]=-x(x+1);
又f(x+1)=2f(x),
∴f(x)=
f(x+1)=-
x(x+1).
故答案为:-
x(x+1).
∴f(x+1)=(x+1)[1-(x+1)]=-x(x+1);
又f(x+1)=2f(x),
∴f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:-
| 1 |
| 2 |
点评:本题考查了求函数解析式的知识,是基础题,其中正确理解函数的概念是解决问题的关键.

练习册系列答案
相关题目
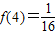 时,求使
时,求使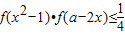 对任意实数x恒成立的参数a的取值范围.
对任意实数x恒成立的参数a的取值范围. 时,求使
时,求使 对任意实数x恒成立的参数a的取值范围.
对任意实数x恒成立的参数a的取值范围.