题目内容
已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x= ,动点P在直线l上的射影为Q,且4
,动点P在直线l上的射影为Q,且4 .
.(1)求点P的轨迹C的方程;
(2)设A、B是轨迹C上两个动点,
 ,λ∈R,∠AOB=θ,请把△AOB的面积S表示为θ的函数,并求此函数的定义域.
,λ∈R,∠AOB=θ,请把△AOB的面积S表示为θ的函数,并求此函数的定义域.
【答案】分析:(1)设P(x,y),根据4 ,可得
,可得
即 ,化简可得y2=6x;
,化简可得y2=6x;
(2)由 知A、B、M共线,设AB的方程为x=my+2,与抛物线方程联立消去x得y2-6my-12=0,从而可得△AOB的面积S表示为θ的函数,利用S=
知A、B、M共线,设AB的方程为x=my+2,与抛物线方程联立消去x得y2-6my-12=0,从而可得△AOB的面积S表示为θ的函数,利用S= ,可确定函数的定义域.
,可确定函数的定义域.
解答: 解:(1)设P(x,y)
解:(1)设P(x,y)
∵4 .
.
∴
∴
整理得y2=6x;
(2)由 知A、B、M共线,设AB的方程为x=my+2,
知A、B、M共线,设AB的方程为x=my+2,
与抛物线方程联立消去x得y2-6my-12=0,
y1y2=-12,x1x2= =4,
=4, =-8.
=-8.
S= =-4tanθ.
=-4tanθ.
因为S= ,
,
所以-4tanθ≥ ,
,
即tanθ≤ ,解得
,解得 .
.
点评:本题以向量条件为载体,考查抛物线的方程,考查三角形面积的计算,正确转化是解题的关键.
 ,可得
,可得
即
 ,化简可得y2=6x;
,化简可得y2=6x;(2)由
 知A、B、M共线,设AB的方程为x=my+2,与抛物线方程联立消去x得y2-6my-12=0,从而可得△AOB的面积S表示为θ的函数,利用S=
知A、B、M共线,设AB的方程为x=my+2,与抛物线方程联立消去x得y2-6my-12=0,从而可得△AOB的面积S表示为θ的函数,利用S= ,可确定函数的定义域.
,可确定函数的定义域.解答:
 解:(1)设P(x,y)
解:(1)设P(x,y)∵4
 .
.∴

∴

整理得y2=6x;
(2)由
 知A、B、M共线,设AB的方程为x=my+2,
知A、B、M共线,设AB的方程为x=my+2,与抛物线方程联立消去x得y2-6my-12=0,
y1y2=-12,x1x2=
 =4,
=4, =-8.
=-8.S=
 =-4tanθ.
=-4tanθ.因为S=
 ,
,所以-4tanθ≥
 ,
,即tanθ≤
 ,解得
,解得 .
.点评:本题以向量条件为载体,考查抛物线的方程,考查三角形面积的计算,正确转化是解题的关键.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
 已知平面直角坐标系xOy上的区域D由不等式组
已知平面直角坐标系xOy上的区域D由不等式组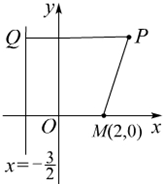 已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=
已知平面直角坐标系xOy上的定点M(2,0)和定直线l:x=