题目内容
已知p：5＜m＜8，q：方程
+
=1表示双曲线，则p是q的（ ）
| x2 |
| m-2 |
| y2 |
| 5-m |
分析：本题考查的判断充要条件的方法，我们可以根据充要条件的定义进行判断
解答：解：∵q：方程
+
=1表示双曲线
∴（m-2）（5-m）＜0，
∴m＞5或m＜2．
又∵p：5＜m＜8
∵p⇒q，
故p是q的充分条件；反过来不成立
∴则p是q的充分不必要条件
故选A
| x2 |
| m-2 |
| y2 |
| 5-m |
∴（m-2）（5-m）＜0，
∴m＞5或m＜2．
又∵p：5＜m＜8
∵p⇒q，
故p是q的充分条件；反过来不成立
∴则p是q的充分不必要条件
故选A
点评：判断充要条件的方法是：
①若p⇒q为真命题且q⇒p为假命题，则命题p是命题q的充分不必要条件；
②若p⇒q为假命题且q⇒p为真命题，则命题p是命题q的必要不充分条件；
③若p⇒q为真命题且q⇒p为真命题，则命题p是命题q的充要条件；
④若p⇒q为假命题且q⇒p为假命题，则命题p是命题q的即不充分也不必要条件．
⑤判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．
①若p⇒q为真命题且q⇒p为假命题，则命题p是命题q的充分不必要条件；
②若p⇒q为假命题且q⇒p为真命题，则命题p是命题q的必要不充分条件；
③若p⇒q为真命题且q⇒p为真命题，则命题p是命题q的充要条件；
④若p⇒q为假命题且q⇒p为假命题，则命题p是命题q的即不充分也不必要条件．
⑤判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
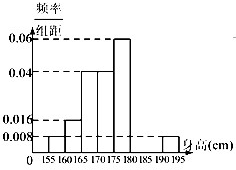从某校高三年级800名男生中随机抽取50名学生测量其身高，据测量被测学生的身高全部在155cm到195cm之间．将测量结果按如下方式分成8组：第一组[155，160），第二组[160，165），…，第八组[190，195]，如图是按上述分组得到的频率分布直方图的一部分．已知：第1组与第8组的人数相同，第6组、第7组和第8组的人数依次成等差数列．?（1）求下列频率分布表中所标字母的值，并补充完成频率分布直方图；
| 分组 | 频数 | 频率 | 频率/组距 |
| … | … | … | … |
| [180，185） | x | y | z |
| [185，190） | m | n | p |
| … | … | … | … |