题目内容
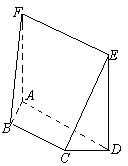
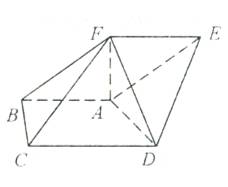 如图,在五面体
如图,在五面体![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为平行四边形,
为平行四边形,![]() 平面
平面![]() ,
,![]() .求:
.求:
(Ⅰ)直线![]() 到平面
到平面![]() 的距离;
的距离;
(Ⅱ)二面角![]() 的平面角的正切值.
的平面角的正切值.
(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]()
解析:
解法一:
(Ⅰ)![]() 平面
平面![]() ,
, ![]() AB到面
AB到面![]() 的距离等于点A到面
的距离等于点A到面![]() 的距离,过点A作
的距离,过点A作![]() 于G,因
于G,因![]()
![]() ∥
∥![]() ,故
,故![]() ;又
;又![]()
![]() 平面
平面![]() ,由三垂线定理可知,
,由三垂线定理可知,![]() ,故
,故![]() ,知
,知![]() ,所以AG为所求直线AB到面
,所以AG为所求直线AB到面![]() 的距离。
的距离。
在![]() 中,
中,![]()
由![]() 平面
平面![]() ,得
,得![]() AD,从而在
AD,从而在![]() 中,
中,![]()
![]()
![]() 。即直线
。即直线![]() 到平面
到平面![]() 的距离为
的距离为![]() 。
。
 (Ⅱ)由己知,
(Ⅱ)由己知,![]() 平面
平面![]() ,得
,得![]() AD,又由
AD,又由![]() ,知
,知![]() ,故
,故![]() 平面ABFE
平面ABFE
![]()
![]() ,所以,
,所以,![]() 为二面角
为二面角![]() 的平面角,记为
的平面角,记为![]() .
.
在![]() 中,
中, ![]() ,由
,由![]() 得,
得,![]() ,从而
,从而![]() 。
。
在![]() 中,
中, ![]() ,故
,故![]()
所以二面角![]() 的平面角的正切值为
的平面角的正切值为![]() .
.
解法二:
(Ⅰ)如图以A点为坐标原点,![]() 的方向为
的方向为![]() 的正方向建立空间直角坐标系数,则A(0,0,0)
的正方向建立空间直角坐标系数,则A(0,0,0)
C(2,2,0) D(0,2,0) 设![]() 可得
可得![]() ,由
,由![]() .即
.即![]() ,解得
,解得![]()
![]()
![]() ∥
∥![]() ,
,
![]() 面
面![]() ,所以直线AB到面
,所以直线AB到面![]() 的距离等于点A到面
的距离等于点A到面![]() 的距离。设A点在平面
的距离。设A点在平面![]() 上的射影点为
上的射影点为![]() ,则
,则![]() 因
因![]() 且
且![]() ,而
,而![]() ,
,![]() ,此即
,此即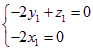 解得
解得![]() ① ,知G点在
① ,知G点在![]() 面上,故G点在FD上.
面上,故G点在FD上.
![]() ∥
∥![]() ,
,![]() 故有
故有![]() ② 联立①,②解得,
② 联立①,②解得, ![]()
![]()
![]() 为直线AB到面
为直线AB到面![]() 的距离. 而
的距离. 而![]() 所以
所以![]()
(Ⅱ)因四边形![]() 为平行四边形,则可设
为平行四边形,则可设![]() ,
,![]() .由
.由![]() 得
得![]() ,解得
,解得![]() .即
.即![]() .故
.故![]()
由![]() ,
,![]() 因
因![]() ,
,![]() ,故
,故![]() 为二面角
为二面角![]() 的平面角,
的平面角,
又![]()
![]() ,
,![]() ,
,![]() ,所以
,所以![]() w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()

练习册系列答案
相关题目
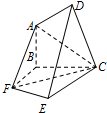 (2012•安徽模拟)如图,在五面体中,平面ABCD⊥平面BFEC,Rt△ACD、RtACB、Rt△FCB、Rt△FCE为全等直角三角形,AB=AD=FB=FE=1,斜边AC=FC=2.
(2012•安徽模拟)如图,在五面体中,平面ABCD⊥平面BFEC,Rt△ACD、RtACB、Rt△FCB、Rt△FCE为全等直角三角形,AB=AD=FB=FE=1,斜边AC=FC=2. 中,四边形
中,四边形 是正方形,
是正方形, 平面
平面 ∥
∥

 与
与 所成角的余弦值;
所成角的余弦值; 平面
平面 ;
; 的正切值。
的正切值。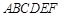 中,四边形
中,四边形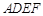 是正方形,
是正方形,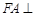 平面
平面 ,
,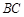 ∥
∥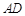 ,
,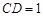 ,
, 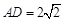 ,
,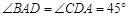 。
。
 与
与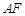 所成角的余弦值;
所成角的余弦值;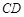 ⊥平面
⊥平面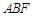 ;
;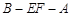 的正切值
的正切值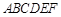 中,四边形
中,四边形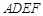 是正方形,
是正方形,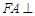 平面
平面 ,
,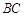 ∥
∥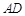 ,
,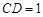 ,
, 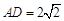 ,
,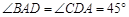 。
。
 与
与 所成角的余弦值;
所成角的余弦值; ⊥平面
⊥平面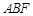 ;
;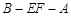 的正切值
的正切值