题目内容
过抛物线y2=4x的焦点F的直线交该抛物线于A,B两点.若|AF|=3,则|BF|= .
【答案】
【解析】由题意知,抛物线的焦点F的坐标为(1,0),又|AF|=3,由抛物线定义知,点A到准线x=-1的距离为3
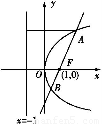
∴点A的横坐标为2.
将x=2代入y2=4x得y2=8,
由图知点A的纵坐标y=2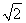
,
∴A(2,2),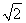
∴直线AF的方程为y=2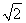(x-1).
由
解得
或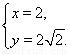
由图知,点B的坐标为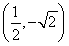
,
∴|BF|=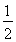
-(-1)=.
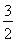练习册系列答案
小学数学口算题卡脱口而出系列答案
优秀生应用题卡口算天天练系列答案
浙江之星课时优化作业系列答案
相关题目
倾斜角为
的直线过抛物线y2=4x的焦点且与抛物线交于A，B两点，则|AB|=（ ）
| π |
| 4 |
A、
| ||
B、8
| ||
| C、16 | ||
| D、8 |
过抛物线y2=4x的焦点F的直线交抛物线于A、B两点，点O是坐标原点，若|AF|=5，则△AOB的面积为（ ）
| A、5 | ||
B、
| ||
C、
| ||
D、
|