题目内容
若函数f(x)= +2(a-1)x+2在区间
+2(a-1)x+2在区间 内递减,那么实数a的取值范围为( )
内递减,那么实数a的取值范围为( )
| A.a≤-3 | B.a≥-3 | C.a≤5 | D.a≥3 |
A
解析试题分析:由题知 ,所以
,所以 ,故选A.
,故选A.
考点:二次函数单调性

练习册系列答案
相关题目
命题 函数
函数 在区间
在区间 上是增函数;命题
上是增函数;命题
 函数的值域为R.则
函数的值域为R.则 是
是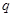 成立的( )
成立的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
下列函数中,既是奇函数又是增函数的为( )
A.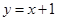 | B.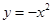 | C.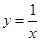 | D.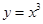 |
若函数 满足
满足 ,且
,且 时,
时, ,函数
,函数 ,则函数
,则函数 在区间
在区间 内的零点的个数为( )
内的零点的个数为( )
| A.8 | B.9 | C.10 | D.13 |
已知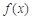 是定义在
是定义在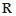 上的奇函数,当
上的奇函数,当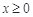 时,
时,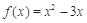 .则函数
.则函数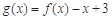
的零点的集合为
A.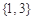 | B.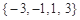 |
C.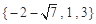 | D.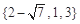 |
 ,则
,则 ( )
( )
A. | B. | C. | D. |
已知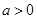 且
且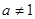 ,函数
,函数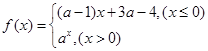 满足对任意实数
满足对任意实数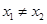 ,都有
,都有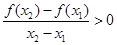 成立,则
成立,则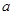 的取值范围是 ( )
的取值范围是 ( )
A.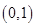 | B.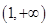 | C.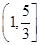 | D.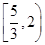 |
函数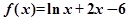 的零点一定位于区间( )
的零点一定位于区间( )
A.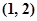 | B.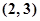 | C.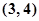 | D.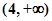 |
 ; q:
; q:
 ,
, 是
是 的充分不必要条件,求实数
的充分不必要条件,求实数 的取值范围。
的取值范围。