题目内容
a,b,c,d成等比数列,a+b,b+c,c+d均不为零,求证:a+b,b+c,c+d成等比数列.
证法一:由已知得b2=ac,c2=bd,![]() ,
,
即bc=ad.
而(b+c)2=b2+c2+2bc=ac+bd+bc+bc
=ac+bd+bc+ad=(a+b)(c+d),
而a+b,b+c,c+d均不为零,故a+b,b+c,c+d成等比数列.
证法二:设b=aq,c=aq2,d=aq3.
![]() =q,
=q,
∴a+b,b+c,c+d成等比数列.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
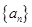 与公比为
与公比为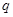 的等比数列
的等比数列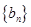 有相同的首项,同时满足
有相同的首项,同时满足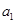 ,
,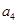 ,
,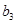 成等比,
成等比, ,
,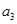 ,
,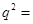 ( )
( )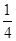 B.
B.
 C.
C.
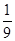 D.
D.
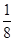
 是公差不为O的等差数列,
是公差不为O的等差数列,  且
且 成等比数列,则
成等比数列,则 项和
项和
 B.
B. C.
C.  D.
D.