题目内容
对于函数f(x),若存在x∈R,使f(x)=x成立,则称x为f(x)的不动点.如果函数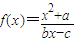 有且仅有两个不动点0、2.
有且仅有两个不动点0、2.(1)求b,c满足的关系式;
(2)若c=2时,相邻两项和不为零的数列{an}满足
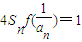 (Sn是数列{an}的前n项和),求证:
(Sn是数列{an}的前n项和),求证: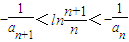 .
.
【答案】分析:(1)利用f(x)的不动点的定义,结合函数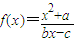 有且仅有两个不动点0,2,可得0,2是方程(1-b)x2+cx+a=0的两个根,利用韦达定理,可求b,c满足的关系式;
有且仅有两个不动点0,2,可得0,2是方程(1-b)x2+cx+a=0的两个根,利用韦达定理,可求b,c满足的关系式;
(2)确定an=-n,于是要证的不等式即为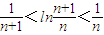 从而我们可以考虑证明不等式:
从而我们可以考虑证明不等式: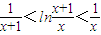 (x>0).
(x>0).
解答:(1)解:设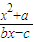 =x,可得(1-b)x2+cx+a=0,(b≠1).
=x,可得(1-b)x2+cx+a=0,(b≠1).
由于函数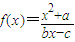 有且仅有两个不动点0,2,故0,2是方程(1-b)x2+cx+a=0的两个根,
有且仅有两个不动点0,2,故0,2是方程(1-b)x2+cx+a=0的两个根,
∴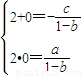
解得a=0,b=1+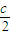 ;
;
(2)证明:c=2时,b=1+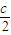 =2,∴
=2,∴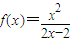
∴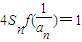 可得2Sn=an-
可得2Sn=an-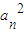 ,
,
当n≥2时,2Sn-1=an-1-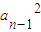 .
.
两式相减得(an+an-1)(an-an-1+1)=0,所以an=-an-1或an-an-1=-1.
当n=1时,2a1=a1-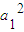 ,∴a1=-1,
,∴a1=-1,
若an=-an-1,则a2=1与an≠1矛盾,所以an-an-1=-1,从而an=-n,
于是要证的不等式即为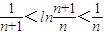
从而我们可以考虑证明不等式: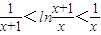 (x>0)
(x>0)
令1+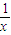 =t,x>0,则t>1,x=
=t,x>0,则t>1,x=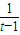 .
.
再令g(t)=t-1-lnt,g′(t)=1- ,由t∈(1,+∞)知g′(t)>0,
,由t∈(1,+∞)知g′(t)>0,
所以当t∈(1,+∞)时,g(t)单调递增,所以g(t)>g(1)=0,于是t-1>lnt,即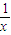 >ln
>ln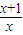 ,x>0…①.
,x>0…①.
令h(t)=lnt-1+ ,h′(t)=
,h′(t)= -
-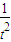 =
=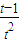 ,当t∈(1,+∞)时,h(t)单调递增,所以h(t)>h(1)=0,
,当t∈(1,+∞)时,h(t)单调递增,所以h(t)>h(1)=0,
于是lnt>1- ,即ln
,即ln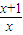 >
>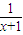 ,x>0…②.
,x>0…②.
由①②可知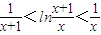 (x>0)
(x>0)
∴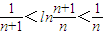
点评:本题主要考查利用导数研究函数的单调性,数列与不等式的综合应用,考查学生分析解决问题的能力,属于难题.
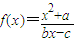 有且仅有两个不动点0,2,可得0,2是方程(1-b)x2+cx+a=0的两个根,利用韦达定理,可求b,c满足的关系式;
有且仅有两个不动点0,2,可得0,2是方程(1-b)x2+cx+a=0的两个根,利用韦达定理,可求b,c满足的关系式;(2)确定an=-n,于是要证的不等式即为
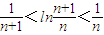 从而我们可以考虑证明不等式:
从而我们可以考虑证明不等式: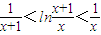 (x>0).
(x>0).解答:(1)解:设
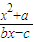 =x,可得(1-b)x2+cx+a=0,(b≠1).
=x,可得(1-b)x2+cx+a=0,(b≠1).由于函数
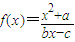 有且仅有两个不动点0,2,故0,2是方程(1-b)x2+cx+a=0的两个根,
有且仅有两个不动点0,2,故0,2是方程(1-b)x2+cx+a=0的两个根,∴
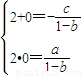
解得a=0,b=1+
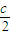 ;
;(2)证明:c=2时,b=1+
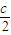 =2,∴
=2,∴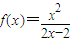
∴
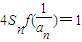 可得2Sn=an-
可得2Sn=an-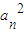 ,
,当n≥2时,2Sn-1=an-1-
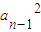 .
.两式相减得(an+an-1)(an-an-1+1)=0,所以an=-an-1或an-an-1=-1.
当n=1时,2a1=a1-
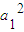 ,∴a1=-1,
,∴a1=-1,若an=-an-1,则a2=1与an≠1矛盾,所以an-an-1=-1,从而an=-n,
于是要证的不等式即为
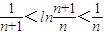
从而我们可以考虑证明不等式:
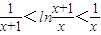 (x>0)
(x>0)令1+
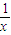 =t,x>0,则t>1,x=
=t,x>0,则t>1,x=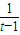 .
.再令g(t)=t-1-lnt,g′(t)=1-
 ,由t∈(1,+∞)知g′(t)>0,
,由t∈(1,+∞)知g′(t)>0,所以当t∈(1,+∞)时,g(t)单调递增,所以g(t)>g(1)=0,于是t-1>lnt,即
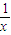 >ln
>ln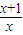 ,x>0…①.
,x>0…①.令h(t)=lnt-1+
 ,h′(t)=
,h′(t)= -
-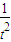 =
=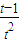 ,当t∈(1,+∞)时,h(t)单调递增,所以h(t)>h(1)=0,
,当t∈(1,+∞)时,h(t)单调递增,所以h(t)>h(1)=0,于是lnt>1-
 ,即ln
,即ln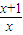 >
>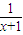 ,x>0…②.
,x>0…②.由①②可知
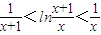 (x>0)
(x>0)∴
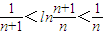
点评:本题主要考查利用导数研究函数的单调性,数列与不等式的综合应用,考查学生分析解决问题的能力,属于难题.

练习册系列答案
相关题目