题目内容
设函数 ,且以
,且以 为最小正周期.
为最小正周期.
(Ⅰ)求f(x)的最大值,并求能使f(x)取得最大值时的x的集合.
(Ⅱ)已知 ,求sinα的值.
,求sinα的值.
解:(Ⅰ)整理得:
而 =
=
∴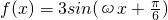
∵f(x)的周期为 ,
,
∴ =
= ?ω=4.
?ω=4.
故f(x)=3sin(4x+ ).…(4分)
).…(4分)
当4x+ =2kπ+
=2kπ+ ,即x=
,即x= ,(k∈Z)时,ymax=3.
,(k∈Z)时,ymax=3.
此时x的集合为 .…(8分)
.…(8分)
(Ⅱ)∵f( )=3sin(
)=3sin(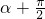 )=3cosα,
)=3cosα,
∴3cosα= ,即cosα=
,即cosα= .…(10分)
.…(10分)
∴sinα=± .…(12分)
.…(12分)
分析:(I)首先用辅助角公式将f(x)整理为: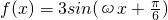 ,利用正弦函数关于周期的公式可以算出ω=4.再用正弦函数的最值及相应最值点x取值的结论得:当4x+
,利用正弦函数关于周期的公式可以算出ω=4.再用正弦函数的最值及相应最值点x取值的结论得:当4x+ =2kπ+
=2kπ+ 时,函数取到最大值3,并由此可得取最大值时x的集合.
时,函数取到最大值3,并由此可得取最大值时x的集合.
(II)根据(I)的表达式,将x= 代入,结合正余弦的诱导公式得cosα=
代入,结合正余弦的诱导公式得cosα= ,最后根据同角三角函数的平方关系得到sina的值.
,最后根据同角三角函数的平方关系得到sina的值.
点评:本题考查了三角函数中的恒等变换应用,着重考查了辅助角公式,三角函数的图象与性质和同角三角函数的关系等等,属于中档题.

而
 =
=
∴
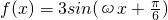
∵f(x)的周期为
 ,
,∴
 =
= ?ω=4.
?ω=4.故f(x)=3sin(4x+
 ).…(4分)
).…(4分)当4x+
 =2kπ+
=2kπ+ ,即x=
,即x= ,(k∈Z)时,ymax=3.
,(k∈Z)时,ymax=3.此时x的集合为
 .…(8分)
.…(8分)(Ⅱ)∵f(
 )=3sin(
)=3sin(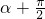 )=3cosα,
)=3cosα,∴3cosα=
 ,即cosα=
,即cosα= .…(10分)
.…(10分)∴sinα=±
 .…(12分)
.…(12分)分析:(I)首先用辅助角公式将f(x)整理为:
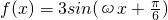 ,利用正弦函数关于周期的公式可以算出ω=4.再用正弦函数的最值及相应最值点x取值的结论得:当4x+
,利用正弦函数关于周期的公式可以算出ω=4.再用正弦函数的最值及相应最值点x取值的结论得:当4x+ =2kπ+
=2kπ+ 时,函数取到最大值3,并由此可得取最大值时x的集合.
时,函数取到最大值3,并由此可得取最大值时x的集合.(II)根据(I)的表达式,将x=
 代入,结合正余弦的诱导公式得cosα=
代入,结合正余弦的诱导公式得cosα= ,最后根据同角三角函数的平方关系得到sina的值.
,最后根据同角三角函数的平方关系得到sina的值.点评:本题考查了三角函数中的恒等变换应用,着重考查了辅助角公式,三角函数的图象与性质和同角三角函数的关系等等,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
 ,且以
,且以 为最小正周期.
为最小正周期. 的值;
的值;  ,求
,求 的值.
的值. ,且以
,且以 为最小正周期。
为最小正周期。 的解析式;
的解析式; 求
求 的值。
的值。 ,且以
,且以 为最小正周期.
为最小正周期. ,求sinα的值.
,求sinα的值. ,且以
,且以 为最小正周期.
为最小正周期. ,求sinα的值.
,求sinα的值.