题目内容
已知数列{an}满足:a2=1, ,则an=
,则an=
- A.

- B.

- C.
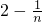
- D.

A
分析:由已知可得, ,结合a2=1,可求a1,,进而利用叠加法可求数列的通项公式
,结合a2=1,可求a1,,进而利用叠加法可求数列的通项公式
解答:∵
∴ ;;;l
;;;l
∵a2=1,∴
∴

…

把上面n-1个式子相加可得,

故选A
点评:本题主要考查由递推公式推导数列的通项公式,其中解题的关键是利用递推的规律利用叠加,但叠加时要注意写出的式子是n-1个而不是n个,这是解题中容易出现错误的地方.
分析:由已知可得,
 ,结合a2=1,可求a1,,进而利用叠加法可求数列的通项公式
,结合a2=1,可求a1,,进而利用叠加法可求数列的通项公式解答:∵

∴
 ;;;l
;;;l∵a2=1,∴

∴


…

把上面n-1个式子相加可得,


故选A
点评:本题主要考查由递推公式推导数列的通项公式,其中解题的关键是利用递推的规律利用叠加,但叠加时要注意写出的式子是n-1个而不是n个,这是解题中容易出现错误的地方.

练习册系列答案
相关题目