题目内容
在
中，
，AB=2，且的面积为
，则BC的长为( )
A． | B．3 | C． | D．7 |
C
解析试题分析：因为在中，，AB=2，且的面积为，所以可得
.所以求得
.由余弦定理可得
.故选C.本小题主要考查余弦定理的使用.
考点：1.三角形的面积公式.2.余弦定理.3.解方程的能力.
练习册系列答案
阶梯计算系列答案
相关题目
若
的内角
满足
，则
（ ）
A． | B． | C． | D． |
，灯塔A在观测站Ｃ的北偏东
，灯塔Ｂ在观测站Ｃ的南偏东
,则灯塔A与灯塔Ｂ的距离为（ ）
B．
C．
Ｄ．
已知
，
，
分别是
的三个内角
，
，
所对的边，若
，
，
，则等于
A． | B． | C． | D．1 |
已知
中，
，
，则角
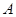等于（ ）
A． | B． | C． | D． |
.已知M是△ABC内的一点，且
，
，若△MBC, △MCA和△MAB的面积分别
，则
的最小值是 ( )
| A．9 | B．18 | C．16 | D．20 |
三角形ABC中,a=15,b=10,A=
,则
（ ）
A． | B．－ | C． | D． |
在△ABC中,
,且
,则内角C的余弦值为( )
| A．1 | B． | C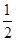． | D． |
