题目内容
已知函数y=2sin（
+
）-1．
（1）用五点法作出它在一个周期上的简图；
（2）该函数的图象可由y=sinx的图象经过怎样的平移和伸缩变换得到？
| x |
| 3 |
| π |
| 4 |
（1）用五点法作出它在一个周期上的简图；
（2）该函数的图象可由y=sinx的图象经过怎样的平移和伸缩变换得到？
分析：（1）根据“五点法”作图的步骤，令相位角
+
分别等0，
，π，
，2π，并求出对应的x，y值，描出五点后，用平滑曲线连接后，即可得到函数y=2sin（
+
）-1的一个周期内的简图．
（2）该函数图象可由y=sinx的图象，按照向左平移，横向伸缩，纵向伸缩，上下平移的方法，即可得到函数的解析式．
| x |
| 3 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| x |
| 3 |
| π |
| 4 |
（2）该函数图象可由y=sinx的图象，按照向左平移，横向伸缩，纵向伸缩，上下平移的方法，即可得到函数的解析式．
解答：解：（1）列表：
函数函数y=2sin（
+
）-1的在区间[
，
]上的图象如下图所示：
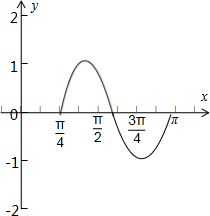
（2）可将y=sinx的图象先向左平移
个单位，得函数y=sin(x+
)的图象；再将此函数图象上的所有点，
横坐标不变，横坐标变为原来的3倍，得函数y=sin（
+
）的图象；
然后又这函数图象上的所有点，横坐标不变，横坐标变为原来的2倍，得函数y=2sin（
+
）的图象；
最后再把这函数图象向下平移1个单位，就得函数y=2sin（
+
）-1的图象．
|
0 |
|
π |
|
2π | ||||||||||
| x |
|
|
|
|
| ||||||||||
y=2sin（
|
0 | 1 | 0 | -1 | 0 |
| x |
| 3 |
| π |
| 4 |
| π |
| 4 |
| 11π |
| 12 |
（2）可将y=sinx的图象先向左平移
| π |
| 4 |
| π |
| 4 |
横坐标不变，横坐标变为原来的3倍，得函数y=sin（
| x |
| 3 |
| π |
| 4 |
然后又这函数图象上的所有点，横坐标不变，横坐标变为原来的2倍，得函数y=2sin（
| x |
| 3 |
| π |
| 4 |
最后再把这函数图象向下平移1个单位，就得函数y=2sin（
| x |
| 3 |
| π |
| 4 |
点评：本题考查的知识点是五点法作函数y=Asin（ωx+φ）的图象，其中描出五个关键点的坐标是解答本题的关键．在解题时才能灵活应用，函数图象的变换注意x 的系数．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
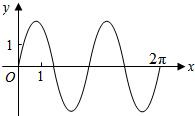已知函数y=2sin（ωx+φ）（ω＞0））在区间[0，2π]的图象如图：那么ω=（ ）| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
已知函数y=2sin（wx+θ）为偶函数，其图象与直线y=2某两个交点的横坐标分别为x1，x2，若|x2-x1|的最小值为π，则该函数在区间（ ）上是增函数．
A、(-
| ||||
B、(-
| ||||
C、(0，
| ||||
D、(
|
下列4个命题：