题目内容
在△ABC中，角A、B、C所对应的边分别为a、b、c，且满足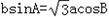
．
（I）求角B的值；
（II）若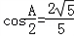
，求sinC的值．
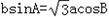．（I）求角B的值；
（II）若
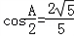，求sinC的值．解：（I）∵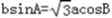
．
由正弦定理得，sinBsinA=
，
∵sinA≠0，即tanB=
，
由于0＜B＜π，所以B=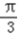
．
（II）cosA=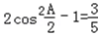
，
因为sinA＞0，故sinA=
，
所以sinC=sin（A+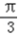
）=
=
．
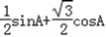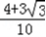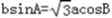．由正弦定理得，sinBsinA=
，∵sinA≠0，即tanB=
，由于0＜B＜π，所以B=
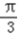．（II）cosA=
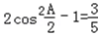，因为sinA＞0，故sinA=
，所以sinC=sin（A+
）==．
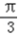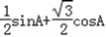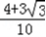练习册系列答案
相关题目
在△ABC中，角A、B、C所对的边分别为a，b，c，若b2+c2-a2=
bc，且b=
a，则下列关系一定不成立的是（ ）
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |