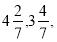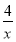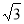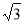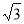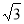题目内容
已知两点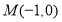 、
、 ,点
,点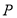 为坐标平面内的动点,满足
为坐标平面内的动点,满足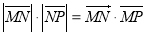 .
.
(1)求动点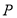 的轨迹方程;
的轨迹方程;
(2)若点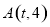 是动点
是动点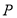 的轨迹上的一点,
的轨迹上的一点,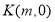 是
是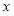 轴上的一动点,试讨论直线
轴上的一动点,试讨论直线
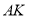 与圆
与圆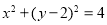 的位置关系.
的位置关系.
(1) (2)当
(2)当 时,直线
时,直线 与圆
与圆 相交;当
相交;当 时,直线
时,直线 与圆
与圆 相切;当
相切;当 时,直线
时,直线 与圆
与圆 相离.
相离.
【解析】
试题分析:(1)直接法求轨迹:根据题意列出方程化简。(2)将点 代入
代入 求
求 ,求出只直线
,求出只直线 方程注意讨论其斜率存在与否。求圆心到直线
方程注意讨论其斜率存在与否。求圆心到直线 的距离,根据距离与半径的关系判断直线与圆的关系。
的距离,根据距离与半径的关系判断直线与圆的关系。
试题解析:(1)设 ,则
,则 ,
,
 ,
,
 . 2分
. 2分
由 ,
,
得2 , 4分
, 4分
化简得 .
.
所以动点 的轨迹方程为
的轨迹方程为 . 5分
. 5分
(2)由点 在轨迹
在轨迹 上,则
上,则 ,解得
,解得 ,即
,即 . 6分
. 6分
当 时,直线
时,直线 的方程为
的方程为 ,此时直线
,此时直线 与圆
与圆 相离. 7分
相离. 7分
当 时,直线
时,直线 的方程为
的方程为 ,即
,即 , 8分
, 8分
圆心 到直线
到直线 的距离
的距离
 ,
,
令

 ,解得
,解得 ;
;
令

 ,解得
,解得 ;
;
令

 ,解得
,解得 .
.
综上所述,当 时,直线
时,直线 与圆
与圆 相交;
相交;
当 时,直线
时,直线 与圆
与圆 相切;
相切;
当 时,直线
时,直线 与圆
与圆 相离. 14分
相离. 14分
考点:1求轨迹方程;2直线与圆的位置关系。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目