题目内容
判断圆x2+y2-2x-1=0与圆x2+y2-8x-6y+7=0的位置关系( )
分析:将两圆化成标准方程,得到它们的圆心和半径,用两点距离公式求出圆心距,最后用圆心距离与两圆的半径和与差进行比较,即可得到两圆的位置关系;
解答:解:将两圆化为标准方程,得C1:(x-1)2+y2=2,C2:(x-4)2+(y-3)2=18
∴圆C1的圆心为(1,0),半径为r1=
;圆C2的圆心为(4,3),半径为r2=3
.
又∵|C1C2|=
=3
,r1+r2=
+3
=4
,r2-r1=3
-
=2
,
可得 r2-r1<|C1C2|<r1+r2
∴两圆相交.
故选:D.
∴圆C1的圆心为(1,0),半径为r1=
| 2 |
| 2 |
又∵|C1C2|=
| (4-1)2+(3-0)2 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
| 2 |
可得 r2-r1<|C1C2|<r1+r2
∴两圆相交.
故选:D.
点评:本题给出两个定圆着重考查了圆的标准方程与一般方程的互化,圆与圆的位的位置关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
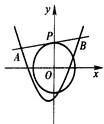 设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点.
设点P(m,n)在圆x2+y2=2上,l是过点P的圆的切线,切线l与函数y=x2+x+k(k∈R)的图象交于A,B两点,点O是坐标原点. A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,
A:如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于点D,BC=4cm,