题目内容
设函数 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).(1)求g(x)的函数表达式;
(2)当a>1时,解不等式
 .
.
【答案】分析:(1)在c2对应的函数g(x)的图象上任意取一点M(x,y),则点M关于点A(2,1)对称点N(4-x,2-y)在函数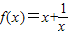 的图象 c1上,化简可得y的解析式,即g(x)的函数表达式.
的图象 c1上,化简可得y的解析式,即g(x)的函数表达式.
(2)当a>1时,由不等式可得0<g(x)< ,化简得0<
,化简得0<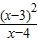 <
< ,即
,即 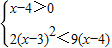 ,由此求得不等式的解集.
,由此求得不等式的解集.
解答:解:(1)在c2对应的函数g(x)的图象上任意取一点M(x,y),则点M关于点A(2,1)对称点N(4-x,2-y)在函数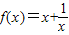 的图象 c1上,
的图象 c1上,
∴2-y=4-x+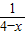 ,
,
∴y=x-2+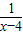 ,即0<g(x)=x-2+
,即0<g(x)=x-2+ .
.
(2)当a>1时,不等式 即 g(x)<
即 g(x)< ,即 0<x-2+
,即 0<x-2+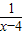 <
< ,
,
化简得0< <
< ,即
,即 .
.
解得 <x<6,即不等式的解集为 {x|
<x<6,即不等式的解集为 {x| <x<6 }.
<x<6 }.
点评:本题主要考查指数不等式对数不等式的解法,函数图象的对称问题的应用,属于中档题.
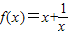 的图象 c1上,化简可得y的解析式,即g(x)的函数表达式.
的图象 c1上,化简可得y的解析式,即g(x)的函数表达式.(2)当a>1时,由不等式可得0<g(x)<
 ,化简得0<
,化简得0<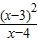 <
< ,即
,即 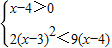 ,由此求得不等式的解集.
,由此求得不等式的解集.解答:解:(1)在c2对应的函数g(x)的图象上任意取一点M(x,y),则点M关于点A(2,1)对称点N(4-x,2-y)在函数
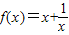 的图象 c1上,
的图象 c1上,∴2-y=4-x+
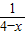 ,
,∴y=x-2+
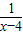 ,即0<g(x)=x-2+
,即0<g(x)=x-2+ .
.(2)当a>1时,不等式
 即 g(x)<
即 g(x)< ,即 0<x-2+
,即 0<x-2+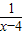 <
< ,
,化简得0<
 <
< ,即
,即 .
.解得
 <x<6,即不等式的解集为 {x|
<x<6,即不等式的解集为 {x| <x<6 }.
<x<6 }.点评:本题主要考查指数不等式对数不等式的解法,函数图象的对称问题的应用,属于中档题.

练习册系列答案
相关题目
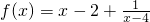 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).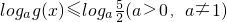 .
.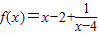 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).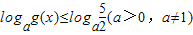 .
.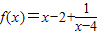 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).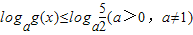 .
.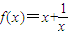 的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).
的图象为c1,c1关于点A(2,1)对称的图象为c2,c2对应的函数为g(x).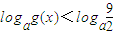 .
.