题目内容
已知数列{an}满足：a1为正整数，an+1=
，如果a1+a2+a3=29，则a1=________．
5
分析：根据题意对an分奇数与偶数讨论，结合a1+a2+a3=29，可求得答案．
解答：∵数列{an}中a1为正整数，an+1=，如果a1+a2+a3=29，
∴若a1为奇数，则a2=3a1+1为偶数，
∴a3=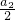
，
∴a1+a2+a3=a1+（3a1+1）+
（3a1+1）=29，
∴a1=5；
若a1为偶数，则a2=a1，
若a2为奇数，则a3=3a2+1=
a1+1，
∴a1+a2+a3=a1+a1+（a1+1）=29，解得a1=
与a1为偶数矛盾；
若a2为偶数，a3==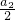
a1，同理可求a1=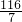
与a1为偶数矛盾．
综上所述，a1=5．
故答案为：5．
点评：本题考查数列的概念及简单表示法，突出考查分段函数的理解与应用，分类讨论思想里面有分类讨论是难点，属于难题．
分析：根据题意对an分奇数与偶数讨论，结合a1+a2+a3=29，可求得答案．
解答：∵数列{an}中a1为正整数，an+1=
，如果a1+a2+a3=29，∴若a1为奇数，则a2=3a1+1为偶数，
∴a3=
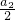，∴a1+a2+a3=a1+（3a1+1）+
（3a1+1）=29，∴a1=5；
若a1为偶数，则a2=
a1，若a2为奇数，则a3=3a2+1=
a1+1，∴a1+a2+a3=a1+
a1+（a1+1）=29，解得a1=与a1为偶数矛盾；若a2为偶数，a3=
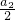=a1，同理可求a1=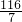与a1为偶数矛盾．综上所述，a1=5．
故答案为：5．
点评：本题考查数列的概念及简单表示法，突出考查分段函数的理解与应用，分类讨论思想里面有分类讨论是难点，属于难题．
练习册系列答案
相关题目