题目内容
15.设x,y满足约束条件$\left\{\begin{array}{l}{2x-3y+6≥0}\\{x-1≤y}\\{x≥0}\\{y≥0}\end{array}\right.$,若目标函数z=ax+by(a>0,b>0)的最大值为8,则$\frac{2}{a}$+$\frac{4}{b}$的最小值为$\frac{49}{4}$.分析 作出不等式对应的平面区域,利用z的几何意义确定取得最大值的条件,然后利用基本不等式即可得到结论.
解答 解:由z=ax+by(a>0,b>0)得$y=-\frac{a}{b}x+\frac{z}{b}$,
∵a>0,b>0,∴直线的斜率$-\frac{a}{b}<0$,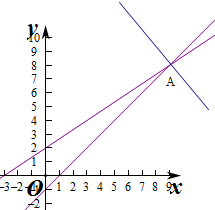
作出不等式对应的平面区域如图:
平移直线得$y=-\frac{a}{b}x+\frac{z}{b}$,由图象可知当直线$y=-\frac{a}{b}x+\frac{z}{b}$经过点A时,直线$y=-\frac{a}{b}x+\frac{z}{b}$的截距最大,此时z最大.
由$\left\{\begin{array}{l}{2x-3y+6=0}\\{x-1=y}\end{array}\right.$,得$\left\{\begin{array}{l}{x=9}\\{y=8}\end{array}\right.$,即A(9,8),
此时目标函数z=ax+by(a>0,b>0)的最大值为8,
即9a+8b=8,∴$\frac{9a}{8}$+b=1,
则$\frac{2}{a}$+$\frac{4}{b}$=($\frac{2}{a}$+$\frac{4}{b}$)($\frac{9a}{8}$+b)=$\frac{18}{8}$+4+$\frac{2b}{a}$+$\frac{36a}{8b}$≥$\frac{25}{4}$+2$\sqrt{\frac{2b}{a}•\frac{36a}{8b}}$=$\frac{25}{4}$+2×3=$\frac{25}{4}$+6=$\frac{49}{4}$,
当且仅当$\frac{2b}{a}$=$\frac{36a}{8b}$,即2b=3a时取等号.
即$\frac{2}{a}$+$\frac{4}{b}$的最小值为$\frac{49}{4}$.
故答案为:$\frac{49}{4}$.
点评 本题主要考查线性规划的基本应用,以及基本不等式的应用,利用数形结合求出目标函数取得最大值的条件是解决本题的关键.

 智慧小复习系列答案
智慧小复习系列答案| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 4 | D. | 1 |
| A. | $\frac{π}{2}$ | B. | π | C. | 2π | D. | 4π |
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
| A. | f(x)=-2sinx | B. | f(x)=2sinx | ||
| C. | f(x)=$\frac{\sqrt{2}}{2}$sin2x | D. | f(x)=$\frac{\sqrt{2}}{2}$(sin2x+cos2x) |
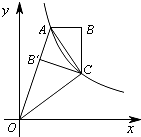 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是2.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得△AB′C,B′点落在OA上,则四边形OABC的面积是2.