题目内容
已知数列 中,
中, (常数
(常数 ),
), 是其前
是其前 项和,且
项和,且 .
.
(1)试确定数列 是否为等差数列,若是,求出其通项公式;若不是,说明理由;
是否为等差数列,若是,求出其通项公式;若不是,说明理由;
(2)令 .
.
(1)数列 是等差数列,
是等差数列, ;(2)见解析.
;(2)见解析.
【解析】
试题分析:(1)令n=1可得 ,即a=0,∴
,即a=0,∴ , 1分
, 1分
 ,可得
,可得 ,当n=2成立, 2分
,当n=2成立, 2分
当n≥3时, ,
, ,
, , ,
, ,
 ,这些式子相乘可得:
,这些式子相乘可得: ,∴
,∴ , 5分
, 5分

显然当n=1,2时满足上式,∴数列 是等差数列,
是等差数列, ; 6分
; 6分
(2)由(1)可知, ,从而可得
,从而可得 . 7分
. 7分
 ,
,
∵ 均大于0,∴
均大于0,∴ . 10分
. 10分
∵ 是关于n的增函数,∴f(n)的最小值为
是关于n的增函数,∴f(n)的最小值为 ,
,
∴ ,
,
故 . 12分
. 12分
考点:考查了等差数列的判定,裂项相消法求和,数列与不等式的综合应用.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 且斜率为k的直线
且斜率为k的直线 与圆
与圆 相交于P、Q两点,则
相交于P、Q两点,则 的值为 .
的值为 .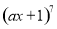 的展开式中,
的展开式中,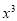 项的系数是
项的系数是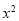 项系数和
项系数和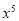 项系数的等比中项,则实数
项系数的等比中项,则实数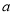 的值为
的值为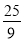 B.
B.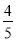 C.
C.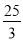 D.
D.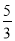
 ,向量
,向量 ,
, ,且
,且 ,则
,则 ___________.
___________. ,
, ,
, ,
, ,
, 中任取两个不同字母,则取到字母
中任取两个不同字母,则取到字母 的概率为 .
的概率为 .