题目内容
设函数f(x)=xsinx在x=x0处取得极值,则(1+x02)cos2x0的值为( )
| A、0 | B、1 | C、2 | D、3 |
分析:先根据函数f(x)=xsinx在x=x0处取得极值可得出x02=tan2x0,代入(x02+1)cos2x0化简求值即可得到所求答案
解答:解:f(x)=xsinx则f′(x)=sinx+xcosx=0
解得tanx=-x,
∴x02=tan2x0,
∴(x02+1)cos2x0=(tan2x0+1)cos2x0=
×cos2x0=1
故答案为:1.
解得tanx=-x,
∴x02=tan2x0,
∴(x02+1)cos2x0=(tan2x0+1)cos2x0=
| cos2x0+sin2x0 |
| cos2x0 |
故答案为:1.
点评:本题主要考查了函数在某点取得极值的条件,解题的关键得出x02=tan2x,从而把求值的问题转化到三角函数中,得以顺利解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
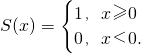 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).