Question

已知二次函数f（x）满足条件：f（0）=1，f（x+1）=f（x）+2x
（1）求f（x）；
（2）若直线y=a与函数y=f（|x|）有4个交点，求实数a的取值范围．

Answer 1

分析：（1）利用待定系数法求二次函数的解析式，由f（0）=1，f（x+1）=f（x）+2x即可确定f（x）．
（2）作出函数y=f（|x|）的图象，利用图象确定实数a的取值范围．

解答：解：（1）设二次函数f（x）=ax²+bx+c，（a≠0），
∵f（0）=1，∴f（0）=c=1，解得c=1，
∴f（x）=ax²+bx+1，（a≠0），
∵f（x+1）=f（x）+2x
∴a（x+1）²+b（x+1）+1=ax²+bx+1+2x，
即ax²+2ax+1+bx+b+1=ax²+bx+1+2x，
∴2a=2，b+1=0，解得a=1，b=-1，
∴f（x）=x²-x+1．
（2）y=f（|x|）=x²-|x|+1=

x2-x+1，x≥0 x2+x+1，x＜0

，
作出函数y=f（|x|）的图象如图：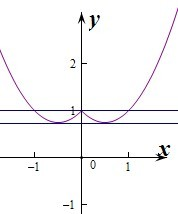
当x=0时，y=f（0）=1，
当x＞时，y=x2-x+1=(x-

1

2

)2+

3

4

，
∴当x=

1

2

时，函数y有最小值，
∴要使直线y=a与函数y=f（|x|）有4个交点，
则

3

4

＜a＜1，
即实数a的取值范围是（

3

4

，1）．

点评：本题主要考查利用待定系数法求二次函数的解析式，以及利用数形结合的方法求函数交点问题，综合性较强．