题目内容
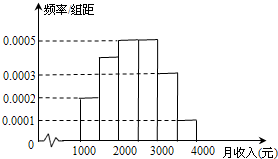 (2013•临沂三模)某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500),单位:元).
(2013•临沂三模)某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500),单位:元).(Ⅰ)估计居民月收入在[1500,2000)的概率;
(Ⅱ)根据频率分布直方图算出样本数据的中位数;
(Ⅲ)若将频率视为概率,从本地随机抽取3位居民(看做有放回的抽样),求月收入在[1500,2000)的居民数X的分布列和数学期望.
分析:(Ⅰ)根据直方图,可得居民月收入在[1500,2000)的概率;
(Ⅱ)根据频率分布直方图知,中位数在[2000,2500),由此可算出样本数据的中位数;
(Ⅲ)由题意知,X~B(3,0.3),求出相应的概率,可得X的分布列和数学期望.
(Ⅱ)根据频率分布直方图知,中位数在[2000,2500),由此可算出样本数据的中位数;
(Ⅲ)由题意知,X~B(3,0.3),求出相应的概率,可得X的分布列和数学期望.
解答:解:(Ⅰ)由题意,居民月收入在[1500,2000)的概率约为1-(0.0002+0.0001+0.0003+0.0005×2)×500=1-0.0016×500=1-0.8=0.2.
(Ⅱ)由频率分布直方图知,中位数在[2000,2500),
设中位数为x,则0.0002×500+0.2+0.0005(x-2000)=0.5,解得x=2400.
(Ⅲ)居民月收入在[1000,2000)的概率为0.0002×500+0.2=0.3,
由题意知,X~B(3,0.3),
因此P(x=0)=
×0.73=0.343,P(x=1)=
×0.72×0.3=0.441,P(x=2)=
×0.7×0.32=0.189,P(x=3)=
×0.33=0.027.
故随机变量X的分布列为
X的数学期望为3×0.3=0.9.
(Ⅱ)由频率分布直方图知,中位数在[2000,2500),
设中位数为x,则0.0002×500+0.2+0.0005(x-2000)=0.5,解得x=2400.
(Ⅲ)居民月收入在[1000,2000)的概率为0.0002×500+0.2=0.3,
由题意知,X~B(3,0.3),
因此P(x=0)=
| C | 0 3 |
| C | 1 3 |
| C | 2 3 |
| C | 3 3 |
故随机变量X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | 0.343 | 0.441 | 0.189 | 0.027 |
点评:本题考查频率分布直方图,考查中位数的计算,考查随机变量X的分布列与数学期望,考查学生的计算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 (2013•临沂三模)甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示,
(2013•临沂三模)甲、乙两名运动员在某项测试中的6次成绩如茎叶图所示, (2013•临沂三模)如图是函数f(x)=x2+ax+b的部分图象,函数g(x)=ex-f'(x)的零点所在的区间是(k,k+1)(k∈z),则k的值为( )
(2013•临沂三模)如图是函数f(x)=x2+ax+b的部分图象,函数g(x)=ex-f'(x)的零点所在的区间是(k,k+1)(k∈z),则k的值为( ) (2013•临沂三模)函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=( )
(2013•临沂三模)函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,则tan∠APB=( )