Question

.已知函数f(x)=-log₂,求f(x)的定义域并讨论它的奇偶性和单调性.

Answer 1

f(x)是奇函数.

f(x)是奇函数，所以f(x)在（-1，0）内单调递减.

解析:

x需满足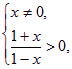由>0得-1<x<1.

    所以函数f(x)的定义域为（-1,0）∪(0,1).

    因为函数f(x)的定义域关于原点对称，且对定义域内的任意x,

    有f(-x)=--log₂=-(-log₂)=-f(x),

    所以f(x)是奇函数.

    研究f(x)在（0，1）内的单调性，任取x₁,x₂∈（0，1），且设x₁<x₂,则

f(x₁)-f(x₂)=-log₂-+log₂=(-)+［log₂(-1)-log₂(-1)］

    由->0,log₂(-1)-log₂(-1)>0得f(x₁)-f(x₂)>0,

    即f(x)在（0,1）内单调递减,

    由于f(x)是奇函数，所以f(x)在（-1，0）内单调递减.