题目内容
8.已知{an}是各项均为正数的等比数列,且a1a2a3=5,a7a8a9=10,则log2(a4a5a6)=$\frac{1}{2}$+log25.分析 由数列{an}是等比数列,a1a2a3,a4a5a6,a7a8a9成等比数列,可得a4a5a6=5$\sqrt{2}$,再利用对数的运算性质可得结论.
解答 解:由等比数列的性质知,a1a2a3,a4a5a6,a7a8a9成等比数列,所以a4a5a6=5$\sqrt{2}$,
所以log2(a4a5a6)=log2(5$\sqrt{2}$)=$\frac{1}{2}$+log25.
故答案为:$\frac{1}{2}$+log25.
点评 本小题主要考查等比数列的性质、指数幂的运算、根式与指数式的互化等知识,着重考查了转化与化归的数学思想.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
3.已知m=loga$\frac{3}{2}$+loga2,n=logb9-logb3,若m<n,则下列结论中,不可能成立的是( )
| A. | 0<b<a<1 | B. | 0<a<b<1 | C. | a>b>1 | D. | 0<a<1<b |
20.三个男生与三个女生站一排,若女生甲不站排头与排尾,三个男生中有且仅有两个男生相邻,则这样的排法数为( )
| A. | 432 | B. | 288 | C. | 216 | D. | 144 |
 为了了解某年级1 000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,被抽取学生的成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为2:8:20,且第二组的频数为8.
为了了解某年级1 000名学生的百米成绩情况,随机抽取了若干学生的百米成绩,被抽取学生的成绩全部介于13秒与18秒之间,将成绩按如下方式分成五组:第一组[13,14);第二组[14,15);…;第五组[17,18].按上述分组方法得到的频率分布直方图如图所示,已知图中从左到右的前3个组的频率之比为2:8:20,且第二组的频数为8.
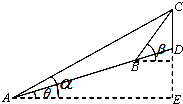 如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.
如图,一山顶有一信号塔CD(CD所在的直线与地平面垂直),在山脚A处测得塔尖C的仰角为α,沿倾斜角为θ的山坡向上前进l米后到达B处,测得C的仰角为β.