Question

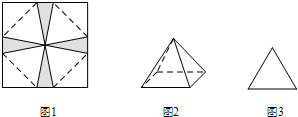
将一张边长为12cm的纸片按如图1所示阴影部分裁去四个全等的等腰三角形，将余下部分沿虚线折成一个有底的正四棱锥模型，如图2放置．若正四棱锥的正视图是正三角形（如图3），则四棱锥的体积是

64 6

3

cm³．

Answer 1

分析：根据正视图形状，得正四棱锥底面边长为a，则它的高h=

3

2

a，斜高h'=a．从而得到图1中正方形的中心O到一个顶点的距离为a+

1

2

a=

3

2

a，结合题中数据可解得a=4

2

，最后用锥体体积公式可算出该四棱锥的体积．

解答：解：∵正四棱锥的正视图是正三角形
∴正四棱锥底面边长为a，则它的高h=

3

2

a，斜高h'=a
在图1中，△ABC是等腰三角形，△OAC是高为a的等腰三角形
∴正方形的中心O到一个顶点的距离为

2

2

×12=a+

1

2

a=

3

2

a，可得a=4

2

由此可得，正四棱锥的底面边长为4

2

，高h=

3

2

×4

2

=2

6

∴四棱锥的体积是V=

1

3

×（4

2

）²×2

6

=

64

3

6

故答案为：

64

3

6

点评：本题将一个正方形沿虚线裁剪，再拼成一个正四棱锥，求它的体积，着重考查了侧面展开图、四棱锥的性质和锥体体积公式等知识，属于基础题．