题目内容
在数列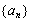 中,
中,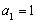 ,
, .
.
(1)设 ,求数列
,求数列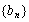 的通项公式;
的通项公式;
(2)求数列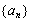 的前
的前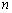 项和
项和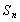 .
.
【答案】
(1) ;(2)
;(2) .
.
【解析】
试题分析:(1)在题中等式两边同时除以 得
得 ,则
,则 ,即
,即 ,利用累加法得
,利用累加法得 ;(2)根据第(1)题求出
;(2)根据第(1)题求出 ,利用分组求和,
,利用分组求和, ,后面括号式子利用错位相加法求得结果.
,后面括号式子利用错位相加法求得结果.
试题解析:(1)由已知得 ,原式同除以
,原式同除以 得
得 ,则
,则 ,即
,即 ,所以
,所以


……

累加,得
所以
由(1)得 ,
,
所以
设 ,①
,①
 ,②
,②
①-②,得

所以 ,
,
所以
考点:1.累加法求通项公式;2.分组求和法和错误相减法求和.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
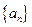 中,
中,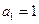 ,
,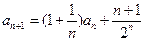 。
。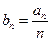 ,求数列
,求数列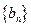 的通项公式;
的通项公式;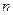 项和
项和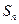 。
。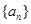 中,
中,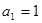 ,
,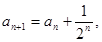 ,
,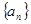 的通项公式;
的通项公式;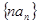 的前
的前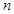 项和
项和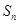 ;
;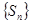 的最小项的值,并证明你的结论。
的最小项的值,并证明你的结论。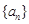 中,
中,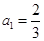 ,
,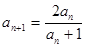 ,
,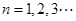
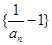 是等比数列; (2)求数列
是等比数列; (2)求数列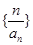 的前n项和。
的前n项和。