题目内容
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,短轴长为2.
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l过 且与椭圆相交于A,B两点,当P是AB的中点时,求直线l的方程.
且与椭圆相交于A,B两点,当P是AB的中点时,求直线l的方程.
解:设椭圆方程为 .
.
(Ⅰ)由已知可得
 .
.
∴所求椭圆方程为 .
.
(Ⅱ)当直线l的斜率存在时,设直线l的方程为 ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),
则 ,
,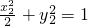 ,两式相减得:
,两式相减得: .
.
∵P是AB的中点,∴ ,
, ,
,
代入上式可得直线AB的斜率为 ,
,
∴直线l的方程为2x-4y+3=0.
当直线l的斜率不存在时,将 代入椭圆方程并解得
代入椭圆方程并解得 ,
, ,
,
这时AB的中点为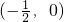 ,∴
,∴ 不符合题设要求.
不符合题设要求.
综上,直线l的方程为2x-4y+3=0.
分析:(Ⅰ)设椭圆方程为 ,由题意可得
,由题意可得 ,解出即可;
,解出即可;
(Ⅱ)分情况进行讨论:当直线l的斜率存在时,利用平方差法:设A(x1,y1),B(x2,y2),代入椭圆方程作差,根据斜率公式、中点坐标公式即可求得斜率,再由点斜式即可求得此时直线方程;当直线斜率不存在时,求出点A、B坐标,检验即可;
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查分类讨论思想,凡涉及弦中点问题一般可考虑“平方差”法,即设出弦端点坐标,代入圆锥曲线方程作差,由中点坐标公式及斜率公式可得弦斜率及中点坐标关系.
 .
. (Ⅰ)由已知可得

 .
. ∴所求椭圆方程为
 .
. (Ⅱ)当直线l的斜率存在时,设直线l的方程为
 ,A(x1,y1),B(x2,y2),
,A(x1,y1),B(x2,y2),则
 ,
,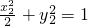 ,两式相减得:
,两式相减得: .
.∵P是AB的中点,∴
 ,
, ,
,代入上式可得直线AB的斜率为
 ,
,∴直线l的方程为2x-4y+3=0.
当直线l的斜率不存在时,将
 代入椭圆方程并解得
代入椭圆方程并解得 ,
, ,
,这时AB的中点为
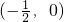 ,∴
,∴ 不符合题设要求.
不符合题设要求.综上,直线l的方程为2x-4y+3=0.
分析:(Ⅰ)设椭圆方程为
 ,由题意可得
,由题意可得 ,解出即可;
,解出即可;(Ⅱ)分情况进行讨论:当直线l的斜率存在时,利用平方差法:设A(x1,y1),B(x2,y2),代入椭圆方程作差,根据斜率公式、中点坐标公式即可求得斜率,再由点斜式即可求得此时直线方程;当直线斜率不存在时,求出点A、B坐标,检验即可;
点评:本题考查直线与圆锥曲线的位置关系、椭圆方程的求解,考查分类讨论思想,凡涉及弦中点问题一般可考虑“平方差”法,即设出弦端点坐标,代入圆锥曲线方程作差,由中点坐标公式及斜率公式可得弦斜率及中点坐标关系.

练习册系列答案
相关题目
 已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.
已知椭圆的中心在坐标原点O,焦点在x轴上,短轴长为2,且两个焦点和短轴的两个端点恰为一个正方形的顶点.过右焦点F与x轴不垂直的直线l交椭圆于P,Q两点.